機械学習への道のり～これから学びたい領域

もう一度関数とは

$y = f(x)$

### y = f(x) ###
# y = ax (a≠0) は x が1つに決まれば y の値も1つに決まるなら
# y は x の関数である
# 関数の仕組みは、x を何らかの規則に従って変換すると y が求まる
# 数式では y = f(x) とあらわす
# 入力値 x を何らかの規則に従って変換した結果、出力値 y がただひとつに決まるのが関数
# f(x) = 2x * 3 の場合、f(1) とすると x = 1 となり、解は 5 になる
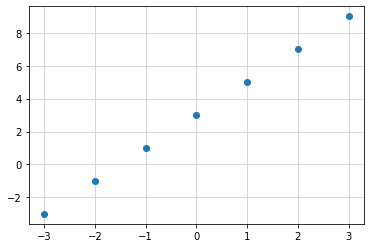
# x = [-3, -2, -1, 0, 1, 2, 3] の場合
# y = [-3, -1 , 1, 3, 5, 7, 9] となる
# x, y の関係をグラフにすると、座標平面上に点が表示される

%matplotlib inline

import matplotlib
import matplotlib.pyplot as plt
import numpy as np
import sympy as sp
import matplotlib.font_manager as fm
fp = fm.FontProperties(fname = 'C:\WINDOWS\Fonts\msgothic.ttc', size = 10)

save_fig_path = "./data/L008-01_1_1.png"

fig = plt.figure()
ax = fig.add_subplot(111)

# 関数の定義
def f(x):
    return 2*x + 3

# x 座標、y 座標
x = np.arange(-3, 4)
y = f(x)

# グラフ
plt.plot(x, y, "o")
plt.grid(color = '0.8')
plt.show()

# グラフをファイルに保存
fig.savefig(save_fig_path)

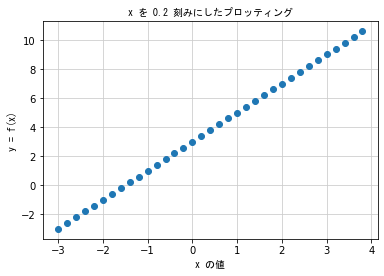
### もっと細かく点を描画する ###

save_fig_path = "./data/L008-01_1_2.png"

fig = plt.figure()
ax = fig.add_subplot(111)

# 関数の定義
def f(x):
    return 2*x + 3

# x 座標、y 座標
x = np.arange(-3, 4, 0.2)
y = f(x)

# グラフ
plt.title('x を 0.2 刻みにしたプロッティング', fontproperties = fp)
plt.xlabel('x の値', fontproperties = fp)
plt.ylabel('y = f(x)', fontproperties = fp)
plt.plot(x, y, "o")
plt.grid(color = '0.8')
plt.show()

# グラフをファイルに保存
fig.savefig(save_fig_path)

一次関数と直線の式

### 一次関数と直線の式 ###
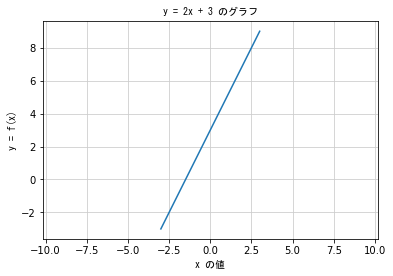
# y = 2x + 3 のように x と y の関係をあらわす式が x の一次式であるとき
# y は x の 一次関数 であるという
# y = ax + b (a≠0) と一般的な式で表せる
# 一次関数のグラフは直線を描くので、y = ax + b を直線の式ともいう

save_fig_path = "./data/L008-01_1_3.png"

fig = plt.figure()
ax = fig.add_subplot(111)

# 関数の定義
def f(x):
    return 2*x + 3

# x 座標、y 座標
x = np.arange(-3, 4)
y = f(x)

# グラフ
plt.title('y = 2x + 3 のグラフ', fontproperties = fp)
plt.xlabel('x の値', fontproperties = fp)
plt.ylabel('y = f(x)', fontproperties = fp)
plt.plot(x, y)
plt.grid(color = '0.8')
plt.axis('equal')
plt.show()

# グラフをファイルに保存
fig.savefig(save_fig_path)

# 一次関数のグラフは直線を描くが、その逆は成り立たない
# 直線の式だからといって必ずしも一次関数ではない ということになる

save_fig_path = "./data/L008-01_1_4.png"

def func(x):
    return n / m * x

m = 1
n = 0
m = float(m)
n = float(n)

x = []
y = []

for i in range(-6, 7):
    x.append(i)
    y.append(func(i))

# グラフ
plt.title('y = 0', fontproperties = fp)
plt.xlabel('x の値', fontproperties = fp)
plt.ylabel('y の値', fontproperties = fp)
plt.plot(x, y)
plt.grid(color = '0.8')
plt.axis('equal')
plt.show()

# グラフをファイルに保存
fig.savefig(save_fig_path)

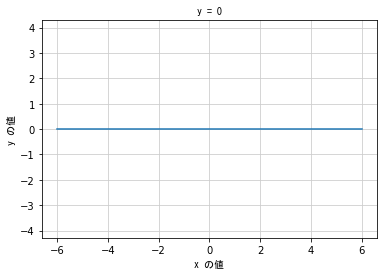
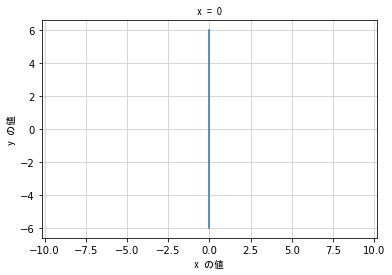
# x = 0 の直線

save_fig_path = "./data/L008-01_1_5.png"

x = [0, 0]
y = [-6, 6]

plt.title('x = 0', fontproperties = fp)
plt.xlabel('x の値', fontproperties = fp)
plt.ylabel('y の値', fontproperties = fp)
plt.plot(x, y)
plt.axis('equal')
plt.grid(color = '0.8')
plt.show()

# グラフをファイルに保存
fig.savefig(save_fig_path)

save_fig_path = "./data/L008-01_1_6.png"

def func(x):
    return n / m * x

m = 1
n = 0
m = float(m)
n = float(n)

x1 = []
y1 = []

for i in range(-10, 11):
    x1.append(i)
    y1.append(func(i))

x2 = [0, 0]
y2 = [-10, 11]

# グラフ
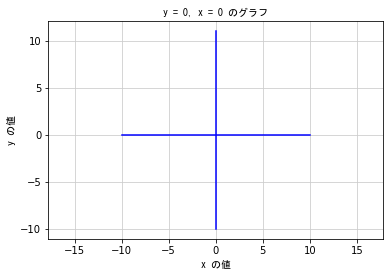
plt.title('y = 0, x = 0 のグラフ', fontproperties = fp)
plt.xlabel('x の値', fontproperties = fp)
plt.ylabel('y の値', fontproperties = fp)
plt.plot(x1, y1, color = 'b')
plt.plot(x2, y2, color = 'b')
plt.grid(color = '0.8')
plt.axis('equal')
plt.show()

# グラフをファイルに保存
fig.savefig(save_fig_path)

save_fig_path = "./data/L008-01_1_7.png"

# 関数の定義
def f(x):
    return 2*x + 3

# x 座標、y 座標
x = np.arange(-3, 5)
y = f(x)

def func(x):
    return n / m * x

m = 1
n = 0
m = float(m)
n = float(n)

x1 = []
y1 = []

for i in range(-9, 10):
    x1.append(i)
    y1.append(func(i))

x2 = [0, 0]
y2 = [-3, 11]

# グラフ
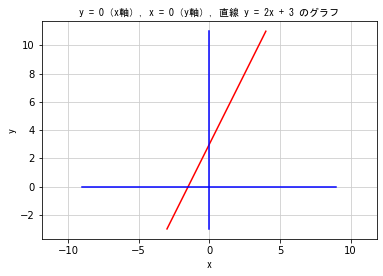
plt.title('y = 0（x軸）, x = 0（y軸）, 直線 y = 2x + 3 のグラフ', fontproperties = fp)
plt.xlabel('x', fontproperties = fp)
plt.ylabel('y', fontproperties = fp)
plt.plot(x, y, color = 'r')
plt.plot(x1, y1, color = 'b')
plt.plot(x2, y2, color = 'b')
plt.grid(color = '0.8')
plt.axis('equal')
plt.show()

# グラフをファイルに保存
fig.savefig(save_fig_path)

関数とグラフ

### 関数とグラフ ###
# x の値が 1つ 決まれば、y の値が 1つ 決まるのが関数
# 関数は直線となる一次関数だけではない
# 関数についてのグラフを見てゆく
#
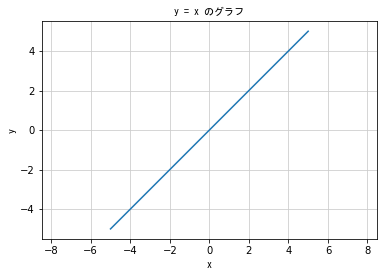
### 比例 ###
# y = ax (a≠0)
# 比例とは一次関数の特別な形で、グラフは常に原点を通る直線となる
# 正比例と言う

%matplotlib inline

import matplotlib
import matplotlib.pyplot as plt
import numpy as np
import sympy as sp
import matplotlib.font_manager as fm
fp = fm.FontProperties(fname = 'C:\WINDOWS\Fonts\msgothic.ttc', size = 10)

save_fig_path = "./data/L008-01_3_1.png"

fig = plt.figure()
ax = fig.add_subplot(111)

# 関数の定義
def f(x):
    return x

# x 座標、y 座標の範囲
x = np.arange(-5, 6)
y = f(x)

# グラフ
plt.title('y = x のグラフ', fontproperties = fp)
plt.xlabel('x', fontproperties = fp)
plt.ylabel('y', fontproperties = fp)
plt.plot(x, y)
plt.grid(color = '0.8')
plt.axis('equal')
plt.show()

# グラフをファイルに保存
fig.savefig(save_fig_path)

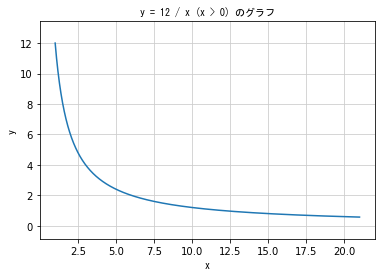
### 反比例 ###
# 1人では12時間、2人では6時間、3人だと4時間で作業がおこなわれる
# 変化する2つの量の積が一定の関係を 反比例 という
# y = a / x
# 反比例の式は一次関数ではない
# f(x) = 12 / x の時の x に対応する y の値
# x = [-6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6]
# Y = [-2, -2.4, -3, -4, -6, -12, -, 12, 6, 4, 3, 2.4, 2]

save_fig_path = "./data/L008-01_3_2.png"

fig = plt.figure()
ax = fig.add_subplot(111)

# 関数の定義
def f(x):
    return 12/x

# x 座標、y 座標の範囲
x = np.arange(1, 21, 0.01)
y = f(x)

# グラフ
plt.title('y = 12 / x (x > 0) のグラフ', fontproperties = fp)
plt.xlabel('x', fontproperties = fp)
plt.ylabel('y', fontproperties = fp)
plt.plot(x, y)
plt.grid(color = '0.8')
plt.axis('equal')
plt.show()

# グラフをファイルに保存
fig.savefig(save_fig_path)

# 0 を範囲に含むとエラーが起きる

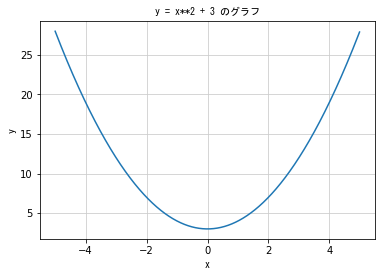
### 二次関数 ###
# 二次関数とは y の値が x の二次式であらわされる関数
# y = ax**2 + bx * c (a≠0)

save_fig_path = "./data/L008-01_3_3.png"

fig = plt.figure()
ax = fig.add_subplot(111)

# 関数の定義
def f(x):
    return x**2 + 3

# x 座標、y 座標の範囲
x = np.arange(-5, 5, 0.01)
y = f(x)

# グラフ
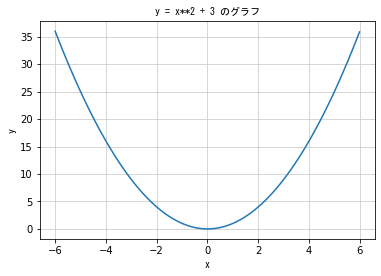
plt.title('y = x**2 + 3 のグラフ', fontproperties = fp)
plt.xlabel('x', fontproperties = fp)
plt.ylabel('y', fontproperties = fp)
plt.plot(x, y)
plt.grid(color = '0.8')
# plt.axis('equal')
plt.show()

# グラフをファイルに保存
fig.savefig(save_fig_path)

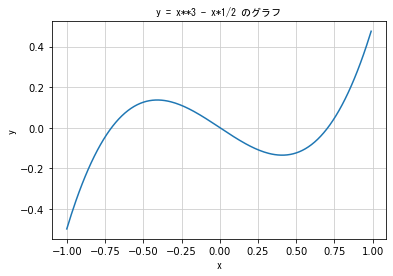
### 三次関数 ###
# y = ax**3 * bx**2 + cx (a≠0) の数式であらわされる関数を三次関数という

%matplotlib inline

import matplotlib
import matplotlib.pyplot as plt
import numpy as np
import sympy as sp
import matplotlib.font_manager as fm
fp = fm.FontProperties(fname = 'C:\WINDOWS\Fonts\msgothic.ttc', size = 10)

save_fig_path = "./data/L008-01_3_4.png"

fig = plt.figure()
ax = fig.add_subplot(111)

# 関数の定義
def f(x):
    return x**3 - 1/2*x

# x 座標、y 座標の範囲
x = np.arange(-1, 1, 0.01)
y = f(x)

# グラフ
plt.title('y = x**3 - x*1/2 のグラフ', fontproperties = fp)
plt.xlabel('x', fontproperties = fp)
plt.ylabel('y', fontproperties = fp)
plt.plot(x, y)
plt.grid(color = '0.8')
# plt.axis('equal')
plt.show()

# グラフをファイルに保存
fig.savefig(save_fig_path)

# 範囲の中で x の小さくするとグラフが滑らかになる

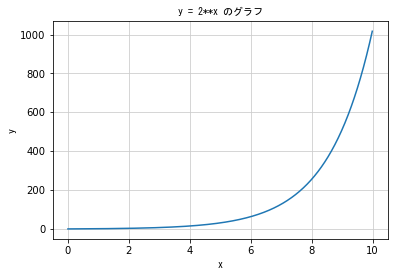
### 指数関数 ###
# 指数関数の式は y = a**x (a>0, a≠1)

save_fig_path = "./data/L008-01_3_5.png"

fig = plt.figure()
ax = fig.add_subplot(111)

# 関数の定義
def f(x):
    return 2**x

# x 座標、y 座標の範囲
x = np.arange(0, 10, 0.01)
y = f(x)

# グラフ
plt.title('y = 2**x のグラフ', fontproperties = fp)
plt.xlabel('x', fontproperties = fp)
plt.ylabel('y', fontproperties = fp)
plt.plot(x, y)
plt.grid(color = '0.8')
# plt.axis('equal')
plt.show()

# グラフをファイルに保存
fig.savefig(save_fig_path)

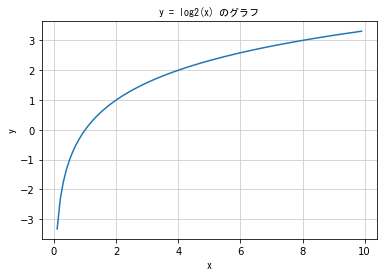
### 対数関数 ###
# log_a x (a>0, a≠0)

save_fig_path = "./data/L008-03_5.png"

fig = plt.figure()
ax = fig.add_subplot(111)

x = np.arange(0.1, 10, 0.1)
y = np.log2(x)

# グラフ
plt.title('y = log2(x) のグラフ', fontproperties = fp)
plt.xlabel('x', fontproperties = fp)
plt.ylabel('y', fontproperties = fp)
plt.plot(x, y)
plt.grid(color = '0.8')
# plt.axis('equal')
plt.show()

# グラフをファイルに保存
fig.savefig(save_fig_path)

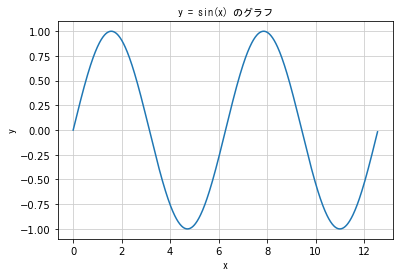
### 三角関数 ###
# 直角三角形で直角以外の角のひとつを θ とすると、三辺の比は 角θ できまる
# これを 角θ の関数とみたものが三角関数
# y = sinθ に注目して、θ を x として y = sin x のグラフを描くと正弦波になる

save_fig_path = "./data/L008-01_3_6.png"

fig = plt.figure()
ax = fig.add_subplot(111)

x = np.radians(np.arange(0, 720))
y = np.sin(x)

# グラフ
plt.title('y = sin(x) のグラフ', fontproperties = fp)
plt.xlabel('x', fontproperties = fp)
plt.ylabel('y', fontproperties = fp)
plt.plot(x, y)
plt.grid(color = '0.8')
# plt.axis('equal')
plt.show()

# グラフをファイルに保存
fig.savefig(save_fig_path)

save_fig_path = "./data/L008-01_3_7.png"

fig = plt.figure()
ax = fig.add_subplot(111)

x = np.radians(np.arange(0, 720))
y = np.cos(x)

# グラフ
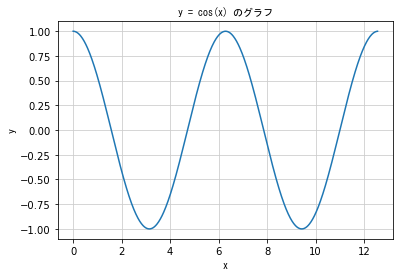
plt.title('y = cos(x) のグラフ', fontproperties = fp)
plt.xlabel('x', fontproperties = fp)
plt.ylabel('y', fontproperties = fp)
plt.plot(x, y)
plt.grid(color = '0.8')
# plt.axis('equal')
plt.show()

# グラフをファイルに保存
fig.savefig(save_fig_path)

save_fig_path = "./data/L008-01_3_8.png"

fig = plt.figure()
ax = fig.add_subplot(111)

x = np.radians(np.arange(0, 360))
y = np.tan(x)

# グラフ
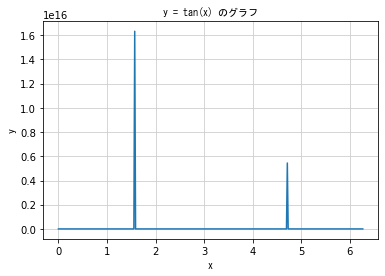
plt.title('y = tan(x) のグラフ', fontproperties = fp)
plt.xlabel('x', fontproperties = fp)
plt.ylabel('y', fontproperties = fp)
plt.plot(x, y)
plt.grid(color = '0.8')
# plt.axis('equal')
plt.show()

# グラフをファイルに保存
fig.savefig(save_fig_path)

変化の割合

### 変化の割合 ###
### 関数と変化の割合 ###
# 変化の割合は x が 1 増えると y の値がどれだけ増えるか
# 変化の割合 = yの増分　/ xの増分 で求められる
# 一次関数は直線のため、どこで調べても変化の割合は同値
# 曲線を描く場合はどうなるか
# Y = x**2 の場合は x が正の値の場合 1 増えると y の値は 1,4,9 ... と増加する
# x が負の値の場合は x が増えると y の値は減少する
# 曲線を描く関数は、変化の割合は一定ではない

%matplotlib inline

import matplotlib
import matplotlib.pyplot as plt
import numpy as np
import sympy as sp
import matplotlib.font_manager as fm
fp = fm.FontProperties(fname = 'C:\WINDOWS\Fonts\msgothic.ttc', size = 10)

save_fig_path = "./data/L008-02_1.png"

fig = plt.figure()
ax = fig.add_subplot(111)

# 関数の定義
def f(x):
    return x**2

# x 座標、y 座標の範囲
x = np.arange(-6, 6, 0.01)
y = f(x)

# グラフ
plt.title('y = x**2 + 3 のグラフ', fontproperties = fp)
plt.xlabel('x', fontproperties = fp)
plt.ylabel('y', fontproperties = fp)
plt.plot(x, y)
plt.grid(color = '0.8')
# plt.axis('equal')
plt.show()

# グラフをファイルに保存
# グラフをファイルに保存
fig.savefig(save_fig_path)

### ちょっとだけ微分 ###
# y = f(x) のグラフ上に 点A と h だけ離れた 点B がある
# 点A の座標を (a,f(a)) とすると 点B の座標は (a + h, f(a + h)) となる
# 点A から 点B までの y の変化の割合は (f(a+h)-f(a)) / h となる
# 点B を 点A に近づけてゆくと h の値は 0 に近づいてゆく
# 極限までに近づくと 直線AB は 点A を通って y = f(x) が描く曲線に接する接線となる
# このときの 直線AB の傾きを lim_h→0 (f(a+h) - f(a)/h) とあらわしこの式を 微分係数 という
# lim_h→0 は h が限り無く 0 に近づくとき という意味で、どんなに h を小さくしても 0 になることはない

### 曲線の接線を描画する ###
# 微分するとは　x の値をほんの少しずつ動かしながら y の値がどう変化するかを調べること
# ある点における微分係数を見つけることができる
# f(x) = x**2 のグラフ

import sympy as sp
sp.init_printing()

# f(x) = x**2
x = sp.Symbol('x')
fx = x**2
display(fx)

# グラフを描画
sp.plot(fx)

\[\displaystyle x^{2}\]

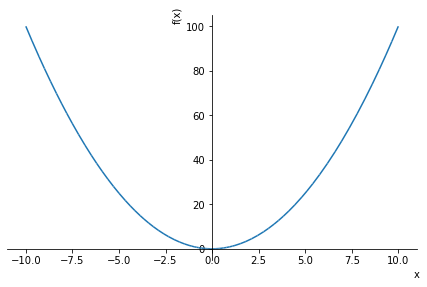
<sympy.plotting.plot.Plot at 0x169d222b610>

### f(x) = x**2 を微分する ##
# SymPy の diff() を使い sp.diff(fx) と記述するだけで、fx に定義されている式を微分できる

sp.diff(fx)

# 微分係数を求めるための式

\[\displaystyle 2 x\]

# 微分係数は y = f(x) のある点における接線の傾き
# x = 3 のときの傾きは、得られた式に 3 を代入すると求められる

sp.diff(fx).subs(x,3)

\[\displaystyle 6\]

### f(x) = x**2 の x = 3 における接線 ###
# f(x) = x**2 を微分した結果、x = 3 での接線の傾きは 6 ということがわかった
# あとは 接点(x1, y1) の座標がわかれば y = a(x - x1) + y1 を使って接線の式が求められる

# f(x) = x**2
x = sp.Symbol('x')
fx = x**2
display(fx)

# 接点の座標
x1 = 3
y1 = fx.subs(x, x1)
display(sp.diff(fx))

# 微分係数（x1 における接線の傾き）
a = sp.diff(fx).subs(x, x1)
display(sp.diff(fx))

# 接線の式（（x1, y1）を通って傾きが a の直線）
y = a * (x -x1) + y1
display(y)

# グラフを描画
sp.plot(fx, y)

\[\displaystyle x^{2}\]

\[\displaystyle 2 x\]

\[\displaystyle 2 x\]

\[\displaystyle 6 x - 9\]

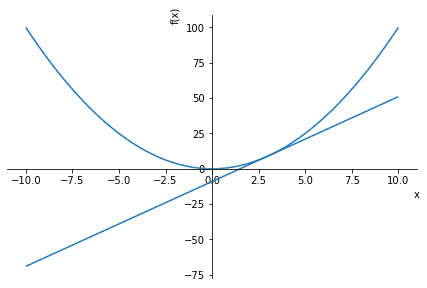
<sympy.plotting.plot.Plot at 0x169d261d9a0>

機械学習のおはなし

### 機械学習で解決できる課題 ###
# AI や 機械学習、ディープ・ラーニング をきちんと定義するのは難しい
# 機械学習 は AI の中のひとつの技術 であり コンピューターが大量のデータを解析して問題解決に役立つ何らかのパターンを見つけること とする
# そのための方法に 教師なし学習 と 教師あり学習 がある
# 大量の顔画像データ（顔写真）があるとして、学習方法の違いを見てみる
#
# 教師なし学習は、大量の顔写真をコンピュータに与えて、特徴量や共通点、パターンを見つける方法
# その中のひとつ クラスタリング は、得られた特徴を利用して似ているデータをグループ化する手法
# 同じグループに分類されたデータから、その集団の持つ意味、子どものグループ、高齢者のグループなどを考えるのは人間の仕事
#
# 教師なし学習は、顔写真と一緒に盛会ラベルを与えて、その特徴やパターンを学習する方法
# 正解ラベルとして年齢を与えて学習させた場合、新たな顔写真を与えたときに20代、30代のように年齢別に分類する
# 回帰 という手法を利用すると この人は27.3歳 といった年齢の推定をすることができる
#
### 学習するの意味 ###
# 最高気温とジュースの販売本数の散布図を描き、データの傾向を最も良く顕す直線の式を求めた
# この直線の式を回帰式といった
# この回帰式を求めるのが 機械学習 の 線形回帰 モデルである
# 回帰式を求めるために 最小二乗法 を用いた
# 直線の傾き a と切片 b の値を少しずつ調整する処理を 500,000回 繰り返した
# この作業を機械学習では 学習する という
# 機械学習では 傾きa や 切片b の代わりに 重み、パラメータ という言葉を使う
# 学習とは、実データと予測値とのずれが小さくなるように何度も何度も計算を繰り返し、最終的に最適な重み（パラメータ）を見付ける作業である
#
### 損失関数とは ###
# 予測した値が実データとどれだけズレているかを示す
# モデルの 性能の悪さ を示す指標
# ずれ の二乗和が大きいときは 回帰式の精度 が悪いことになる
# 精度の良いモデル（回帰式）とは、損失関数（ずれ の二乗和）の値が最小になるモデルである
# 精度を高める（損失関数が ゼロ に近づく）ために、重みを何度も繰り返し調整することが 学習 である
# 回帰式を求めるプログラムから設定した仮の回帰直線からスタートして最終的な回帰直線を得られるまでのずれの二乗和の変化をあらわすグラフ

%matplotlib inline

import matplotlib
import matplotlib.pyplot as plt
import random

# データ
dx = [28, 26, 28, 27, 27, 20, 26, 22, 23, 19, 26, 23, 25, 21, 20, 18, 24, 19, 24, 25]
dy = [111, 97, 102, 105, 108, 74, 116, 92, 112, 88, 116, 101, 93, 74, 87, 71, 94, 67, 105, 99]

# 初期値
a = 0.0    # 直線の傾き
b = 0.0    # 切片

# y = 0 との ずれ の二乗和

min_res = 0.0
for i in range(20):
    y = a * dx[i] + b
    min_res += (dy[i] - y)**2
print(min_res)

dat=[]    # ずれ の二乗和の最小値
for i in range(500000):
    # 傾きと切片の更新量を決定
    wa = (random.random() - 0.5) * 0.001
    wb = (random.random() - 0.5) * 0.001

    # ずれ の二乗和
    res = 0
    for j in range(20):
        y = (a + wa) * dx[j] + (b + wb)
        res += (dy[j] - y)**2

    # 値を更新
    if res < min_res:
        min_res = res    # 仮の最小値
        a = a + wa       # 傾き
        b = b + wb       # 切片
    dat.append(min_res)  # 最小値を追加
print(a, b, min_res)

# グラフを表示
plt.figure(figsize = (12, 4))
plt.plot(dat)
plt.show()

# Matplotlib.Pyplot モジュールで描画するグラフは、特別な指定をしない限り決まった大きさになる
# 上のプログラムは、figure() を利用した
# figure オプションには、幅と高さをタプル型で与える
# 単位は インチ
# plot()、scatter() でグラフを描画する前に実行する必要がある

187050.0
3.821715550517188 5.598597051695401 1444.6670121793827