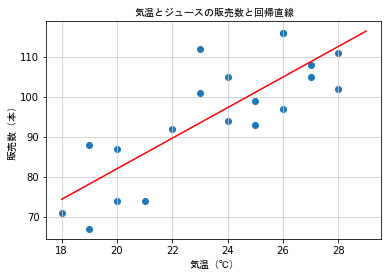
7 多数の点の傾向を示す直線¶
散布図を描く¶
2点から等しい距離にある点を集めると直線になる
3点から等しい距離にある点は1点しかない
4点以上になると全ての点から等しい距離にある位置は求められない
ぴったり等しい点が存在しないとしても、なるべく等しくなる点なら見つけられそう
どれだけ沢山の点があっても、なるべく等しくなる点(線)を見つけることができる
沢山のデータをグラフ上に表す散布図を作り、その上で沢山の点の近くを通るような直線を引く
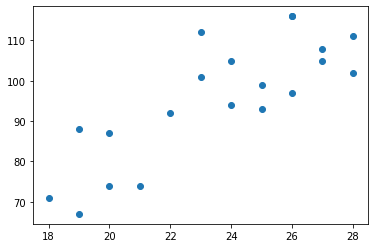
散布図を描く(正の相関)¶
気温が上がるとジュースがよく売れる、背が高いと足のサイズも大きい、数学が得意だと物理の成績も良いどれも何となくそうかも知れないと思える
このような場合は散布図を描いてみる
何となくそうかも知れない事象を数学的に説明できるようになる
散布図は、2つあるデータのいずれかの要素を横軸に、もう一方の要素を縦軸に取る
それぞれの値が交わる位置に点を置く作業をデータの個数だけ繰り返す
# 気温(dx)とジュース(dy)の販売本数のデータを元にして散布図を描く
# -*- coding: utf-8 -*-
%matplotlib inline
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
# グラフ画像の保存先ファイルパス
save_fig_path = "./data/L007-01_1.png"
fig = plt.figure()
ax = fig.add_subplot(111)
# データ
dx = [28, 26, 28, 27, 27, 20, 26, 22, 23, 19, 26, 23, 25, 21, 20, 18, 24, 19, 24, 25]
dy = [111, 97, 102, 105, 108, 74, 116, 92, 112, 88, 116, 101, 93, 74, 87, 71, 94, 67, 105, 99]
# 散布図を描画
plt.scatter(dx, dy)
plt.show()
# グラフをファイルに保存
fig.savefig(save_fig_path)
csvファイル からデータを読み込む¶
散布図の元になるデータは数が多いことが一般的で、プログラミングの時に入力するのは大変な作業となる
データの区切りにカンマを挿入したテキストファイルである csvファイルを利用すると良い
csvファイルは、データとカンマだけの単純なフォーマットのため扱いが簡単で、多くのアプリケーションでデータの受け渡しに利用されている
# -*- coding: utf-8 -*-
%matplotlib inline
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
import csv
# ファイルを開く
f = open('./data/score.csv')
# ファイルから1行ずつ読み込んでリストに追加
dx = []
dy = []
for row in csv.reader(f):
dx.append(int(row[0]))
dy.append(int(row[1]))
# ファイルを閉じる
f.close()
print(dx)
print(dy)
[28, 26, 28, 27, 27, 20, 26, 22, 23, 19, 26, 23, 25, 21, 20, 18, 24, 19, 24, 25]
[111, 97, 102, 105, 108, 74, 116, 92, 112, 88, 116, 101, 93, 74, 87, 71, 94, 67, 105, 99]
ファイルからデータを読み込むにはファイルを開かなければならない
open(‘./data/score.csv’) でファイルを開いている
ファイル名だけ指定すると読み取り専用として開くことができる
for row in csv.reader(f):
ファイルから 1行 読み込んで 変数row に代入するという処理をファイルの先頭行から最終行まで繰り返す命令
1行読むたびに 変数row には [‘28’, ‘111’] というデータが代入されるが、これは文字列になっている
文字列を数値に変換する必要がある
dx.append(int(row[0]))dx.append(int(row[1]))
int() を使って数値に変換している
ファイルの読み込みが終わると close() でファイルを閉じる
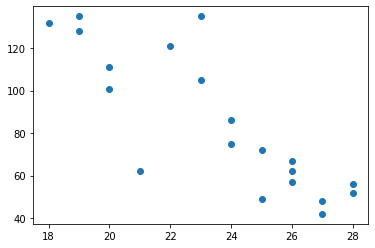
### 散布図を描く(負の相関) ###
# -*- coding: utf-8 -*-
%matplotlib inline
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
import csv
# ファイルを開く
f = open('./data/score_re.csv')
# ファイルから1行ずつ読み込んでリストに追加
dx = []
dy = []
for row in csv.reader(f):
dx.append(int(row[0]))
dy.append(int(row[1]))
# ファイルを閉じる
f.close()
print(dx)
print(dy)
[28, 26, 28, 27, 27, 20, 26, 22, 23, 19, 26, 23, 25, 21, 20, 18, 24, 19, 24, 25]
[56, 62, 52, 48, 42, 101, 57, 121, 105, 128, 67, 135, 49, 62, 111, 132, 75, 135, 86, 72]
# -*- coding: utf-8 -*-
%matplotlib inline
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
import csv
# グラフ画像の保存先ファイルパス
save_fig_path = "./data/L007-01_2.png"
fig = plt.figure()
ax = fig.add_subplot(111)
# ファイルを開く
f = open('./data/score_re.csv')
# ファイルから1行ずつ読み込んでリストに追加
dx = []
dy = []
for row in csv.reader(f):
dx.append(int(row[0]))
dy.append(int(row[1]))
# ファイルを閉じる
f.close()
# 散布図を描画
plt.scatter(dx, dy)
plt.show()
# グラフをファイルに保存
fig.savefig(save_fig_path)
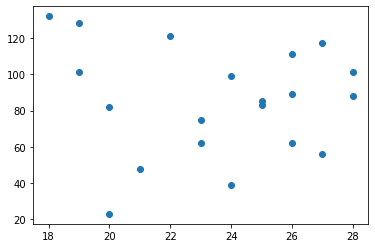
### 散布図を描く(無相関) ###
# -*- coding: utf-8 -*-
%matplotlib inline
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
import csv
# グラフ画像の保存先ファイルパス
save_fig_path = "./data/L007-01_3.png"
fig = plt.figure()
ax = fig.add_subplot(111)
# ファイルを開く
f = open('./data/score_ra.csv')
# ファイルから1行ずつ読み込んでリストに追加
dx = []
dy = []
for row in csv.reader(f):
dx.append(int(row[0]))
dy.append(int(row[1]))
# ファイルを閉じる
f.close()
print(dx)
print(dy)
# 散布図を描画
plt.scatter(dx, dy)
plt.show()
# グラフをファイルに保存
fig.savefig(save_fig_path)
[28, 26, 28, 27, 27, 20, 26, 22, 23, 19, 26, 23, 25, 21, 20, 18, 24, 19, 24, 25]
[101, 62, 88, 117, 56, 23, 89, 121, 62, 128, 111, 75, 83, 48, 82, 132, 99, 101, 39, 85]
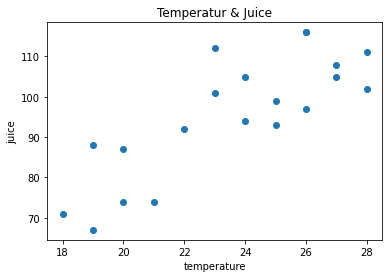
グラフに軸ラベルを追加する¶
軸ラベルを表示するには Matplotlib.Pyplotモジュールの xlabel() と ylabel() を使う
plt.xlabel(‘temperature’)plt.ylabel(‘juice’)
グラフのタイトルを表示留守には title() を使う
plt.title(‘Temperatur & Juice’)
# -*- coding: utf-8 -*-
%matplotlib inline
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
# グラフ画像の保存先ファイルパス
save_fig_path = "./data/L007-01_1.png"
fig = plt.figure()
ax = fig.add_subplot(111)
# ファイルを開く
f = open('./data/score.csv')
# ファイルから1行ずつ読み込んでリストに追加
dx = []
dy = []
for row in csv.reader(f):
dx.append(int(row[0]))
dy.append(int(row[1]))
# ファイルを閉じる
f.close()
plt.title('Temperatur & Juice')
plt.xlabel('temperature')
plt.ylabel('juice')
# 散布図を描画
plt.scatter(dx, dy)
plt.show()
# グラフをファイルに保存
fig.savefig(save_fig_path)
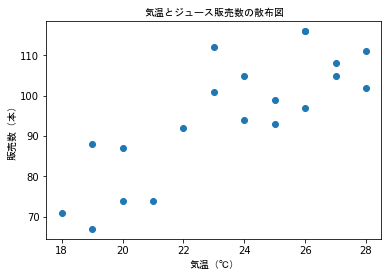
グラフのラベルを日本語で表示する¶
日本語で表示するには mMatplotlib に含まれる Font_Managerモジュールを利用して日本語フォントを指定する必要がある
Windows環境で MSゴシック を利用する
import matplotlib.font_manager as fm
fp = fm.FontProperties(fname = 'C:\WINDOWS\Fonts\msgothic.ttc', size = 10)
plt.title('気温とジュース販売数の散布図', fontproperties = fp)
plt.xlabel('気温(℃)', fontproperties = fp)
plt.ylabel('販売数(本)', fontproperties = fp)
plt.scatter(dx,dy)
plt.show()
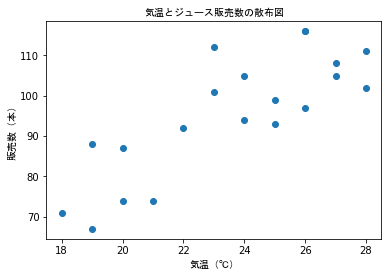
散布図から直線へ¶
# -*- coding: utf-8 -*-
%matplotlib inline
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
import sympy as sp
import csv
import matplotlib.font_manager as fm
fp = fm.FontProperties(fname = 'C:\WINDOWS\Fonts\msgothic.ttc', size = 10)
# ファイルを開く
f = open('./data/score.csv')
# ファイルから1行ずつ読み込んでリストに追加
dx = []
dy = []
for row in csv.reader(f):
dx.append(int(row[0]))
dy.append(int(row[1]))
# ファイルを閉じる
f.close()
plt.title('気温とジュース販売数の散布図', fontproperties = fp)
plt.xlabel('気温(℃)', fontproperties = fp)
plt.ylabel('販売数(本)', fontproperties = fp)
plt.scatter(dx,dy)
plt.show()
# -*- coding: utf-8 -*-
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
import sympy as sp
import math
# 2点の座標
x1 = 18; y1= 70
x2 = 28; y2 = 110
x = sp.Symbol('x') # 未知数 x
x1, y1 = sp.symbols('x1, y1') # 点m の座標
x2, y2 = sp.symbols('x2, y2') # 点n の座標
def func(x):
return ((y2 - y1) / (x2 - x1)) * (x - x1) + y1 # 直線の式
y = func(x).subs({x1:18, y1:68, x2:28, y2:115})
print(y)
47*x/10 - 83/5
# -*- coding: utf-8 -*-
%matplotlib inline
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
import sympy as sp
import csv
import matplotlib.font_manager as fm
fp = fm.FontProperties(fname = 'C:\WINDOWS\Fonts\msgothic.ttc', size = 10)
save_fig_path = "./data/L007-03_1.png"
fig = plt.figure()
ax = fig.add_subplot(111)
# ファイルを開く
f = open('./data/score.csv')
# ファイルから1行ずつ読み込んでリストに追加
dx = []
dy = []
for row in csv.reader(f):
dx.append(int(row[0]))
dy.append(int(row[1]))
# ファイルを閉じる
f.close()
def func(x):
return 47*x/10 - 83/5
x = np.arange(18, 29)
y = func(x)
plt.plot(x, y, color = 'r')
plt.title('散布図と回帰直線(推定)', fontproperties = fp)
plt.xlabel('気温(℃)', fontproperties = fp)
plt.ylabel('販売数(本)', fontproperties = fp)
plt.scatter(dx,dy)
plt.show()
# グラフをファイルに保存
fig.savefig(save_fig_path)
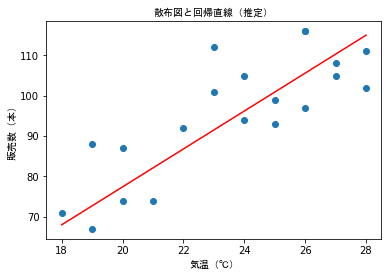
最小二乗法¶
回帰直線は沢山の点の間を通る直線
実データと直線の間には必ず ずれ が生じる
この ずれがすべての点において小さいほどデ-ターの分布傾向と良く似た直線になる
その直線を求める方法のひとつが 最小二乗法 である
最小二乗法では 実データのy座標 と 直線のy座標 との差に注目する
直線を基準とすると y座標の値 との間には + の値と - の値が存在する
これを単純に合計することでは、全体の ずれ を正しく把握できない
実データと直線それぞれの y座標の差を2乗すれば、ずれの大きさがすべてプラスとなる
これを合計した値が最小になるようにくり返し直線を求める
くり返しの回数を 何万回、何十万回も繰り返すことで精度の高い結果を得ることができる
### 実データと直線の ずれ を調べる ###
# 直線と実データのずれを求めるプログラム
# -*- coding: utf-8 -*-
%matplotlib inline
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
import sympy as sp
import csv
import matplotlib.font_manager as fm
fp = fm.FontProperties(fname = 'C:\WINDOWS\Fonts\msgothic.ttc', size = 10)
# ファイルを開く
f = open('./data/score.csv')
# ファイルから1行ずつ読み込んでリストに追加
dx = []
dy = []
for row in csv.reader(f):
dx.append(int(row[0]))
dy.append(int(row[1]))
# ファイルを閉じる
f.close()
# 初期値
a = 0.0
b = 0.0
# 差の二乗和
min_res = 0.0
for i in range(20):
y = a * dx[i] + b
min_res += (dy[i] - y)**2
print(min_res)
187050.0
%matplotlib inline
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
import sympy as sp
import csv
import matplotlib.font_manager as fm
fp = fm.FontProperties(fname = 'C:\WINDOWS\Fonts\msgothic.ttc', size = 10)
dx = np.array([28, 26, 28, 27, 27, 20, 26, 22, 23, 19, 26, 23, 25, 21, 20, 18, 24, 19, 24, 25])
dy = np.array([111, 97, 102, 105, 108, 74, 116, 92, 112, 88, 116, 101, 93, 74, 87, 71, 94, 67, 105, 99])
# 初期値
a = 0.0
b = 0.0
# 差の二乗和
y = a * dx + b
min_res = np.sum(dy - y)**2
print(min_res)
3655744.0
実データと直線との「ずれ」を調べる¶
%matplotlib inline
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
import sympy as sp
import csv
import matplotlib.font_manager as fm
fp = fm.FontProperties(fname = 'C:\WINDOWS\Fonts\msgothic.ttc', size = 10)
dx = np.array([28, 26, 28, 27, 27, 20, 26, 22, 23, 19, 26, 23, 25, 21, 20, 18, 24, 19, 24, 25])
dy = np.array([111, 97, 102, 105, 108, 74, 116, 92, 112, 88, 116, 101, 93, 74, 87, 71, 94, 67, 105, 99])
# 初期値
a = 0.0
b = 0.0
# 差の二乗和
y = a * dx + b
min_res = np.sum(dy - y)**2
print(min_res)
# 結果は、y = 0 の直線との差の二乗和になる
3655744.0
# 数値の ずれ を最小にするための試行をおこなうには乱数を利用する
# Pyton では Randomモジュールの random() を使って、0.0 ~ 1.0 未満の乱数を発生させることができる
import random
for i in range(5):
print(random.random())
0.05222352765262783
0.2038024360956161
0.37948463473348293
0.9618553458751213
0.09601205941757807
# random は正の値しか返さないので、傾きには負の値も必要となる
# random() から返す値から 0.5 を引くと、-0.5 ~ 0.5未満 の乱数を発生することができる
for i in range(5):
print(random.random() - 0.5)
0.3663102052746027
-0.02861943952297219
-0.08441900713042383
0.08741688694125738
-0.39794920217590346
# とても小さな値を無作為に作る
# 傾きの変化を小さくすることで数値の ずれ をさらに小さくする
for i in range(5):
print((random.random() - 0.5) * 0.001)
-0.00020882632896488274
9.217693666000504e-05
-2.532339283725671e-05
-0.0004803246077768294
-0.00011506295285809443
乱数を使って回帰直線を見つける¶
回帰直線を見つけるには
乱数を使って傾きと切片の更新量を決定する
新しい直線の式で実データとの ずれ (差の二乗和)を求める
求めた ずれが仮の最小値よりも小さいときは、仮の最小値と傾き、切片を更新する
import random
for i in range(500000):
# 傾きと切片の更新量を決定
wa = (random.random() - 0.5) * 0.001
wb = (random.random() - 0.5) * 0.001
# 差の二乗和
res = 0
for j in range(20):
y = (a + wa) * dx[j] + (b + wb)
res += (dy[j] - y) ** 2
# 値を更新
if res < min_res:
min_res = res
a = a + wa
b = b + wb
print(a, b, min_res)
# 結果は、傾き、切片、差の二乗和
3.8217154302934895 5.598600190145986 1444.667012179362
回帰直線を予測に使う¶
%matplotlib inline
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
import sympy as sp
import csv
import matplotlib.font_manager as fm
fp = fm.FontProperties(fname = 'C:\WINDOWS\Fonts\msgothic.ttc', size = 10)
dx = np.array([28, 26, 28, 27, 27, 20, 26, 22, 23, 19, 26, 23, 25, 21, 20, 18, 24, 19, 24, 25])
dy = np.array([111, 97, 102, 105, 108, 74, 116, 92, 112, 88, 116, 101, 93, 74, 87, 71, 94, 67, 105, 99])
# 初期値
a = 0.0
b = 0.0
# 差の二乗和
y = a * dx + b
min_res = np.sum(dy - y)**2
print(min_res)
3655744.0
import random
for i in range(500000):
# 傾きと切片の更新量を決定
wa = (random.random() - 0.5) * 0.001
wb = (random.random() - 0.5) * 0.001
# 差の二乗和
res = 0
for j in range(20):
y = (a + wa) * dx[j] + (b + wb)
res += (dy[j] - y) ** 2
# 値を更新
if res < min_res:
min_res = res
a = a + wa
b = b + wb
print(a, b, min_res)
3.8217154058002256 5.598603152979365 1444.6670121793404
save_fig_path = "./data/L007-08_1.png"
fig = plt.figure()
ax = fig.add_subplot(111)
# 回帰直線
def func(x):
return a * x + b # y = ax + b
# 直線用のデータ
x = np.arange(18, 30)
y = func(x)
# 表示
plt.scatter(dx, dy)
plt.plot(x, y, color = 'r')
plt.title('気温とジュースの販売数と回帰直線', fontproperties = fp)
plt.xlabel('気温(℃)', fontproperties = fp)
plt.ylabel('販売数(本)', fontproperties = fp)
plt.grid(color = '0.8')
# plt.axis('equal')
plt.show
# グラフをファイルに保存
fig.savefig(save_fig_path)
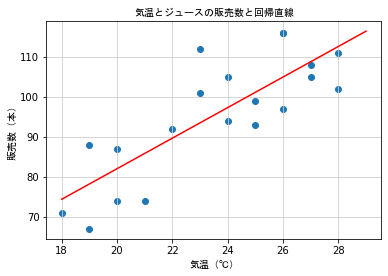
# 回帰直線を元にして最高気温に対してジュースの販売本数を予測する
# exam. 35℃ の場合
y = func(35)
y
139.35864235598726
もっと効率よく直線の式を見つける¶
### もっと効率よく直線の式を見つける ###
# くり返しの回数に応じて乱数の範囲を変化させる
# -0.5 ~ 0.5、-0.005 ~ 0.005、-0.0005 ~ 0.0005 の三段階とする
%matplotlib inline
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
import sympy as sp
import csv
import matplotlib.font_manager as fm
fp = fm.FontProperties(fname = 'C:\WINDOWS\Fonts\msgothic.ttc', size = 10)
dx = np.array([28, 26, 28, 27, 27, 20, 26, 22, 23, 19, 26, 23, 25, 21, 20, 18, 24, 19, 24, 25])
dy = np.array([111, 97, 102, 105, 108, 74, 116, 92, 112, 88, 116, 101, 93, 74, 87, 71, 94, 67, 105, 99])
# 初期値
a = 0.0
b = 0.0
# 差の二乗和
y = a * dx + b
min_res = np.sum(dy - y)**2
print(min_res)
3655744.0
import random
for i in range(100000):
# 傾きと切片の更新量を決定
if i < 10000:
wa = random.random() - 0.5
wb = random.random() - 0.5
elif i < 30000:
wa = (random.random() - 0.5) * 0.01
wb = (random.random() - 0.5) * 0.01
else:
wa = (random.random() - 0.5) * 0.001
wb = (random.random() - 0.5) * 0.001
# 差の二乗和
res = 0
for j in range(20):
y = (a + wa) * dx[j] + (b + wb)
res += (dy[j] - y) ** 2
# 値を更新
if res < min_res:
min_res = res
a = a + wa
b = b + wb
print(a, b, min_res)
3.821715865552417 5.598588408381448 1444.6670121795264
save_fig_path = "./data/L007-08_2.png"
fig = plt.figure()
ax = fig.add_subplot(111)
# 回帰直線
def func(x):
return a * x + b # y = ax + b
# 直線用のデータ
x = np.arange(18, 30)
y = func(x)
# 表示
plt.scatter(dx, dy)
plt.plot(x, y, color = 'r')
plt.title('気温とジュースの販売数と回帰直線', fontproperties = fp)
plt.xlabel('気温(℃)', fontproperties = fp)
plt.ylabel('販売数(本)', fontproperties = fp)
plt.grid(color = '0.8')
# plt.axis('equal')
plt.show
# グラフをファイルに保存
fig.savefig(save_fig_path)
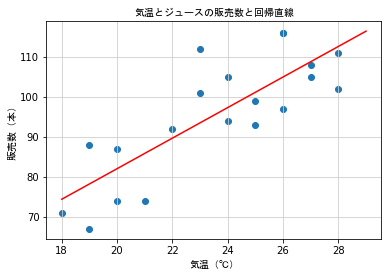
実データを使って最初の直線を決める¶
効率よく回帰直線を求めるために、最初の直線の位置を実データに近い位置にする
もっと効率よく直線の式を見つける¶
くり返しの回数に応じて乱数の範囲を変化させる
-0.5 ~ 0.5、-0.005 ~ 0.005、-0.0005 ~ 0.0005 の三段階とする
%matplotlib inline
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
import sympy as sp
import csv
import random
import matplotlib.font_manager as fm
fp = fm.FontProperties(fname = 'C:\WINDOWS\Fonts\msgothic.ttc', size = 10)
dx = np.array([28, 26, 28, 27, 27, 20, 26, 22, 23, 19, 26, 23, 25, 21, 20, 18, 24, 19, 24, 25])
dy = np.array([111, 97, 102, 105, 108, 74, 116, 92, 112, 88, 116, 101, 93, 74, 87, 71, 94, 67, 105, 99])
# 2点を通る直線の式に、先頭データと最後のデータを代入する
sp.init_printing()
x, y = sp.symbols('x, y')
x1 = 28; y1 = 111
x2 = 25; y2 = 99
y = ((y2 - y1) / (x2 - x1)) * (x - x1) + y1
y
# 初期値
a = 4.0
b = 1.0
# 最初の直線とのずれ
min_res = 0.0
for i in range(20):
y = a * dx[i] + b
min_res += (dy[i] - y)**2
print('ずれの初期値: {0}'.format(min_res))
# 回帰直線を求める
for i in range(200000):
# 傾きと切片の更新量を決定
wa = (random.random() - 0.5) * 0.001
wb = (random.random() - 0.5) * 0.001
# 差の二乗和
res = 0
for j in range(20):
y = (a + wa) * dx[j] + (b + wb)
res += (dy[j] - y)**2
# 値を更新
if res < min_res:
min_res = res
a = a + wa
b = b + wb
print('a: {0}, b: {1}, min_res: {2}'.format(a, b, min_res))
ずれの初期値: 1454.0
a: 3.821716366118323, b: 5.598576979371046, min_res: 1444.667012179611
save_fig_path = "./data/L007-08_3.png"
fig = plt.figure()
ax = fig.add_subplot(111)
# 回帰直線
def func(x):
return a * x + b # y = ax + b
# 直線用のデータ
x = np.arange(18, 30)
y = func(x)
# 表示
plt.scatter(dx, dy)
plt.plot(x, y, color = 'r')
plt.title('気温とジュースの販売数と回帰直線', fontproperties = fp)
plt.xlabel('気温(℃)', fontproperties = fp)
plt.ylabel('販売数(本)', fontproperties = fp)
plt.grid(color = '0.8')
# plt.axis('equal')
plt.show
# グラフをファイルに保存
fig.savefig(save_fig_path)
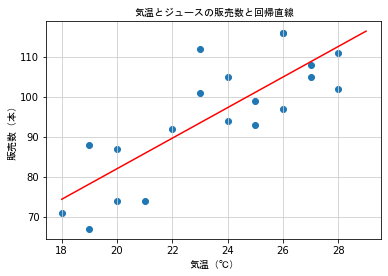
NumPy を使って回帰直線を求める¶
NumPy モジュールの polyfit() を使うことでよりいっそう簡単に回帰直線を求める
%matplotlib inline
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
import sympy as sp
import csv
import random
import matplotlib.font_manager as fm
fp = fm.FontProperties(fname = 'C:\WINDOWS\Fonts\msgothic.ttc', size = 10)
dx = np.array([28, 26, 28, 27, 27, 20, 26, 22, 23, 19, 26, 23, 25, 21, 20, 18, 24, 19, 24, 25])
dy = np.array([111, 97, 102, 105, 108, 74, 116, 92, 112, 88, 116, 101, 93, 74, 87, 71, 94, 67, 105, 99])
# 回帰直線を求める
a, b = np.polyfit(dx, dy, 1)
print('a: {0}, b: {1}'.format(a, b))
a: 3.8217154703291016, b: 5.59860067374965
乱数を使ってくり返し値を求め直すことで最適解を導く手法を 焼きなまし法 あるいは Simulated Annealig = SA という
この手法は、機械学習やデータ・サイエンスの分野でも、キーとなる重要な手法である
save_fig_path = "./data/L007-08_4.png"
fig = plt.figure()
ax = fig.add_subplot(111)
# 回帰直線
def func(x):
return a * x + b # y = ax + b
# 直線用のデータ
x = np.arange(18, 30)
y = func(x)
# 表示
plt.scatter(dx, dy)
plt.plot(x, y, color = 'r')
plt.title('気温とジュースの販売数と回帰直線', fontproperties = fp)
plt.xlabel('気温(℃)', fontproperties = fp)
plt.ylabel('販売数(本)', fontproperties = fp)
plt.grid(color = '0.8')
# plt.axis('equal')
plt.show
# グラフをファイルに保存
fig.savefig(save_fig_path)