6 2点から等距離にある直線

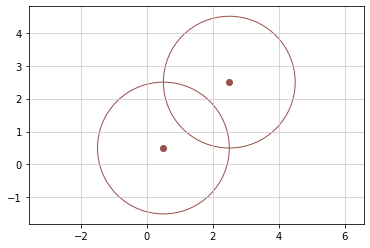
2点から等しい距離に点を打つ

• 2点を中心とした2つの円が交わるように半径を設定して描く

• 2つの円の交点までの中心からの距離は両円の半径となり等しい

# -*- coding: utf-8 -*-
import matplotlib
import matplotlib.pyplot as plt
import numpy as np

# グラフ画像の保存先ファイルパス
save_fig_path = "./data/L006-01_1.png"

fig = plt.figure()
ax = fig.add_subplot(111)

# 中心(0.5,0.5)で半径2の円を描画
circle = plt.Circle((0.5,0.5), 2, ec='#96514d', fill=False)
ax.add_patch(circle)


# 中心(2.5,2.5)で半径2の円を描画
circle = plt.Circle((2.5,2.5), 2, ec='#96514d', fill=False)
ax.add_patch(circle)

plt.grid(color = '0.8')
plt.axis('equal')
plt.scatter(0.5, 0.5, color = '#96514d')
plt.scatter(2.5, 2.5, color = '#96514d')
plt.show()

# グラフをファイルに保存
fig.savefig(save_fig_path)

# -*- coding: utf-8 -*-
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
import sympy as sp
import math

# グラフ画像の保存先ファイルパス
save_fig_path = "./data/L006-01_2.png"

fig = plt.figure()
ax = fig.add_subplot(111)

# 中心(0.5,0.5)で半径2の円を描画
circle = plt.Circle((1, 1), 2, ec='#96514d', fill=False)
ax.add_patch(circle)

# 中心(2.5,2.5)で半径2の円を描画
circle = plt.Circle((3, 3), 2, ec='#96514d', fill=False)
ax.add_patch(circle)

x = [1, 3]
y = x

plt.plot(x, y)
plt.grid(color = '0.8')
plt.axis('equal')
plt.scatter(1, 1, color = '#96514d')
plt.scatter(3, 3, color = '#96514d')
plt.show()

# グラフをファイルに保存
fig.savefig(save_fig_path)

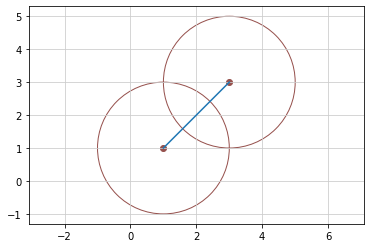
2点から等距離にある直線の式

• 点A（x1, y1）、点B（x2, y2）から等距離にある点P

ピタゴラスの定理により

AP = ((x - x1) ** 2 + ( y- y1) ** 2) ** 0.5

BP = ((x - x2) ** 2 + ( y- y2) ** 2) ** 0.5

AP = BP

2乗して AP ** 2 = BP ** 2 に代入

(x - x1) ** 2 + ( y- y1) ** 2 = (x - x2) ** 2 + ( y- y2) ** 2

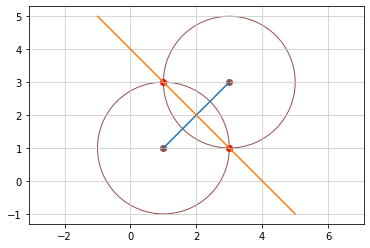
• y について式を解くと 2点から等距離の直線の式 になる

点A（1, 1）、点B（3, 3）として2点から等距離にある直線の式を求める

import sympy as sp
sp.init_printing()

# 記号を定義
x, y = sp.symbols('x, y')

# 値を代入
x1 = 1; y1 = 1
x2 = 3; y2 = 3

# 式を定義（AP ** 2 - BP ** 2 = 0）
expr = ((x - x1) ** 2 + ( y- y1) ** 2) - ((x - x2) ** 2 + ( y- y2) ** 2)
display(expr)
display(sp.simplify(expr))

# 式を y について解く
ans = sp.solve(expr, y)
ans

\[\displaystyle - \left(x - 3\right)^{2} + \left(x - 1\right)^{2} - \left(y - 3\right)^{2} + \left(y - 1\right)^{2}\]

\[\displaystyle 4 x + 4 y - 16\]

\[\displaystyle \left[ 4 - x\right]\]

# -*- coding: utf-8 -*-
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
import sympy as sp
import math

# グラフ画像の保存先ファイルパス
save_fig_path = "./data/L006-01_3.png"

fig = plt.figure()
ax = fig.add_subplot(111)

# 中心(0.5,0.5)で半径2の円を描画
circle = plt.Circle((1, 1), 2, ec='#96514d', fill=False)
ax.add_patch(circle)

# 中心(2.5,2.5)で半径2の円を描画
circle = plt.Circle((3, 3), 2, ec='#96514d', fill=False)
ax.add_patch(circle)

# 2つの円の中心を結ぶ線を描画
x1 = [1, 3]
y1 = x1

# 2つの円の中心と等距離にある直線を描画
def func(x2):
    return 4 - x2

x2 = np.arange(-1, 6)
y2 = func(x2)

plt.plot(x1, y1)
plt.grid(color = '0.8')
plt.axis('equal')
plt.scatter(1, 1, color = '#96514d')
plt.scatter(3, 3, color = '#96514d')
plt.scatter(1, 3, color = 'r')
plt.scatter(3, 1, color = 'r')
plt.show()

# グラフをファイルに保存
fig.savefig(save_fig_path)

### 2点から等距離にある直線の式（一般型） ###

import sympy as sp
sp.init_printing()

# 記号を定義
x, y = sp.symbols('x, y')
x1, y1 = sp.symbols('x1, y1')    # 点A
x2, y2 = sp.symbols('x2, y2')    # 点B

# 式を定義（AP ** 2 - BP ** 2 = 0）
expr = ((x - x1) ** 2 + ( y- y1) ** 2) - ((x - x2) ** 2 + ( y- y2) ** 2)
display(expr)

# 式を y について解く
ans = sp.solve(expr, y)
display(ans)

# 式に値を代入して expr を上書き
expr = expr.subs({x1:1, y1:1, x2:3, y2:3})
display(expr)

# 式を y について解く
ans = sp.solve(expr, y)
ans

\[\displaystyle \left(x - x_{1}\right)^{2} - \left(x - x_{2}\right)^{2} + \left(y - y_{1}\right)^{2} - \left(y - y_{2}\right)^{2}\]

\[\displaystyle \left[ \frac{y_{1}^{2} - y_{2}^{2} + \left(x - x_{1}\right)^{2} - \left(x - x_{2}\right)^{2}}{2 \left(y_{1} - y_{2}\right)}\right]\]

\[\displaystyle - \left(x - 3\right)^{2} + \left(x - 1\right)^{2} - \left(y - 3\right)^{2} + \left(y - 1\right)^{2}\]

\[\displaystyle \left[ 4 - x\right]\]

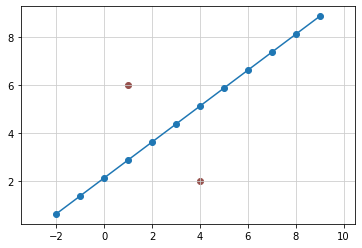
2点から等距離にある直線を描く

# 点(1, 6)、(4, 2)から等距離にある直線を描く

%matplotlib inline
import matplotlib
import matplotlib.pyplot as plt
import numpy as np

# グラフ画像の保存先ファイルパス
save_fig_path = "./data/L006-03_1.png"

fig = plt.figure()
ax = fig.add_subplot(111)

# (1,6)、(4, 2)から等距離にある直線の式
def func(x):
    return 3/4*x + 17/8

# x、yの値
x = np.arange(-2,10)
y = func(x)

# 描画
plt.grid(color = '0.8')
plt.axis('equal')
plt.scatter(1, 6, color = '#96514d')    # 点A
plt.scatter(4, 2, color = '#96514d')    # 点B
plt.plot(x, y, marker='o')    # 2点から等距離にある直線
plt.show()

# グラフをファイルに保存
fig.savefig(save_fig_path)

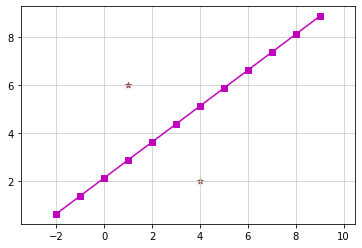
グラフの見た目を変更する

### グラフの見た目を変更する ###
# makerオプション
# o ... ●
# s ... ■
# ^ ... ▲
# x ... ×
# + ... ＋
# * ... ★
#
# colorオプション
# 1文字で指定 ... r, g, b, y, m, c, k, w
# 色名で指定 ... red, green, blue, yellow, magenta, cyan, black, white
# 16進数で指定 ... #******

# 点(1, 6)、(4, 2)から等距離にある直線を描く

%matplotlib inline
import matplotlib
import matplotlib.pyplot as plt
import numpy as np

# グラフ画像の保存先ファイルパス
save_fig_path = "./data/L006-03_1.png"

fig = plt.figure()
ax = fig.add_subplot(111)

# (1,6)、(4, 2)から等距離にある直線の式
def func(x):
    return 3/4*x + 17/8

# x、yの値
x = np.arange(-2,10)
y = func(x)

# 描画
plt.grid(color = '0.8')
plt.axis('equal')
plt.scatter(1, 6, marker='*', color = '#96514d')    # 点A
plt.scatter(4, 2, marker='*', color = '#96514d')    # 点B
plt.plot(x, y, marker='s', color = 'm')    # 2点から等距離にある直線
plt.show()

# グラフをファイルに保存
fig.savefig(save_fig_path)

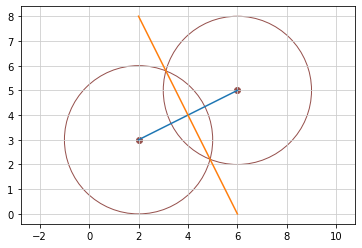
任意の線分の垂直二等分線

• 線分の中点を通ってその線分と直角に交わる直線

垂直二等分線はコンパスを使って簡単に引ける

線分の長さの半分より大きく半径を取る

線分の両端を中心として弧を描く

2つの弧が交わる点を結ぶ線分が垂直二等分線となる

• 2点から等距離にある直線と垂直二等分線は同じ

### 2点から等距離にある直線の式（一般型） ###
#

import sympy as sp
sp.init_printing()

# 記号を定義
x, y = sp.symbols('x, y')
x1, y1 = sp.symbols('x1, y1')    # 点A
x2, y2 = sp.symbols('x2, y2')    # 点B

# 式を定義（AP ** 2 - BP ** 2 = 0）
expr = ((x - x1) ** 2 + ( y- y1) ** 2) - ((x - x2) ** 2 + ( y- y2) ** 2)
display(expr)

# 式を y について解く
ans = sp.solve(expr, y)
display(ans)

# 式に値を代入して expr を上書き
expr = expr.subs({x1:2, y1:3, x2:6, y2:5})
display(expr)

# 式を y について解く
ans = sp.solve(expr, y)
ans

\[\displaystyle \left(x - x_{1}\right)^{2} - \left(x - x_{2}\right)^{2} + \left(y - y_{1}\right)^{2} - \left(y - y_{2}\right)^{2}\]

\[\displaystyle \left[ \frac{y_{1}^{2} - y_{2}^{2} + \left(x - x_{1}\right)^{2} - \left(x - x_{2}\right)^{2}}{2 \left(y_{1} - y_{2}\right)}\right]\]

\[\displaystyle - \left(x - 6\right)^{2} + \left(x - 2\right)^{2} - \left(y - 5\right)^{2} + \left(y - 3\right)^{2}\]

\[\displaystyle \left[ 12 - 2 x\right]\]

import sympy as sp

x = sp.Symbol('x')               # 未知数 x
x1, y1 = sp.symbols('x1, y1')    # 点m の座標
x2, y2 = sp.symbols('x2, y2')    # 点n の座標

y = ((y2 - y1) / (x2 - x1)) * (x - x1) + y1    # 直線の式
y = y.subs({x1:2, y1:3, x2:6, y2:5})            # 式に値を代入
y

\[\displaystyle \frac{x}{2} + 2\]

# -*- coding: utf-8 -*-
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
import sympy as sp
import math

# グラフ画像の保存先ファイルパス
save_fig_path = "./data/L006-01_4.png"

fig = plt.figure()
ax = fig.add_subplot(111)

# 中心(2,3)で半径3の円を描画
circle = plt.Circle((2, 3), 3, ec='#96514d', fill=False)
ax.add_patch(circle)

# 中心(6,5)で半径3の円を描画
circle = plt.Circle((6, 5), 3, ec='#96514d', fill=False)
ax.add_patch(circle)

# 2つの円の中心を結ぶ線を描画
def func(x1):
    return x1/2 +2

x1 = np.arange(2, 7)
y1 = func(x1)

plt.plot(x1, y1)

# 2つの円の中心と等距離にある直線を描画
def func(x2):
    return 12 - 2*x2

x2 = np.arange(2, 7)
y2 = func(x2)

plt.plot(x2, y2)

plt.grid(color = '0.8')
plt.axis('equal')
plt.scatter(2, 3, color = '#96514d')
plt.scatter(6, 5, color = '#96514d')
plt.show()

# グラフをファイルに保存
fig.savefig(save_fig_path)

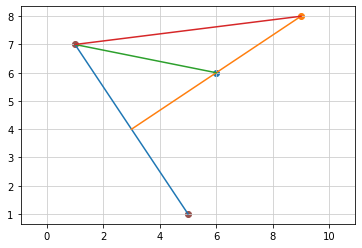
3点から等しい距離にある点

垂直二等分線上の点を中心に円を描く

### 垂直二等分線上の点を中心に円を描く ###
#
# 点A と 点B とを結ぶ直線の式

# -*- coding: utf-8 -*-
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
import sympy as sp
import math

x = sp.Symbol('x')               # 未知数 x
x1, y1 = sp.symbols('x1, y1')    # 点m の座標
x2, y2 = sp.symbols('x2, y2')    # 点n の座標

y = ((y2 - y1) / (x2 - x1)) * (x - x1) + y1    # 直線の式
y = y.subs({x1:1, y1:7, x2:5, y2:1})            # 式に値を代入
y

\[\displaystyle \frac{17}{2} - \frac{3 x}{2}\]

# 垂直二等分線の式

import sympy as sp
sp.init_printing()

# 記号を定義
x, y = sp.symbols('x, y')
x1, y1 = sp.symbols('x1, y1')    # 点A
x2, y2 = sp.symbols('x2, y2')    # 点B

# 式を定義（AP ** 2 - BP ** 2 = 0）
expr = ((x - x1) ** 2 + ( y- y1) ** 2) - ((x - x2) ** 2 + ( y- y2) ** 2)
display(expr)

# 式を y について解く
ans = sp.solve(expr, y)
display(ans)

# 式に値を代入して expr を上書き
expr = expr.subs({x1:1, y1:7, x2:5, y2:1})
display(expr)

# 式を y について解く
ans = sp.solve(expr, y)
ans

\[\displaystyle \left(x - x_{1}\right)^{2} - \left(x - x_{2}\right)^{2} + \left(y - y_{1}\right)^{2} - \left(y - y_{2}\right)^{2}\]

\[\displaystyle \left[ \frac{y_{1}^{2} - y_{2}^{2} + \left(x - x_{1}\right)^{2} - \left(x - x_{2}\right)^{2}}{2 \left(y_{1} - y_{2}\right)}\right]\]

\[\displaystyle - \left(x - 5\right)^{2} + \left(x - 1\right)^{2} + \left(y - 7\right)^{2} - \left(y - 1\right)^{2}\]

\[\displaystyle \left[ \frac{2 x}{3} + 2\right]\]

# 垂直二等分線上の 点C と 点A を結ぶ直線の式

x = sp.Symbol('x')               # 未知数 x
x1, y1 = sp.symbols('x1, y1')    # 点m の座標
x2, y2 = sp.symbols('x2, y2')    # 点n の座標

y = ((y2 - y1) / (x2 - x1)) * (x - x1) + y1    # 直線の式
y = y.subs({x1:6, y1:6, x2:1, y2:7})            # 式に値を代入
y

\[\displaystyle \frac{36}{5} - \frac{x}{5}\]

x = sp.Symbol('x')               # 未知数 x
x1, y1 = sp.symbols('x1, y1')    # 点m の座標
x2, y2 = sp.symbols('x2, y2')    # 点n の座標

y = ((y2 - y1) / (x2 - x1)) * (x - x1) + y1    # 直線の式
y = y.subs({x1:9, y1:8, x2:1, y2:7})            # 式に値を代入
y

\[\displaystyle \frac{x}{8} + \frac{55}{8}\]

# -*- coding: utf-8 -*-
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
import sympy as sp
import math

# グラフ画像の保存先ファイルパス
save_fig_path = "./data/L006-05_1.png"

fig = plt.figure()
ax = fig.add_subplot(111)

# 2つの点A(1,7)、点B(5,1)を結ぶ線を描画
def func(x1):
    return -x1*3/2 + 17/2

x1 = np.arange(1, 6)
y1 = func(x1)

plt.plot(x1, y1)

# 2つの点の垂直二等分線を描画
def func(x2):
    return 2*x2/3 + 2

x2 = np.arange(3, 10)
y2 = func(x2)

plt.plot(x2, y2)

# 2つの点C(6,6)、点A(1,7)を結ぶ線を描画
def func(x3):
    return -x3/5 + 36/5

x3 = np.arange(1, 7)
y3 = func(x3)

plt.plot(x3, y3)

# 2つの点D(9,8)、点A(1,7)を結ぶ線を描画
def func(x4):
    return x4/8 + 55/8

x4 = np.arange(1, 10)
y4 = func(x4)

plt.plot(x4, y4)

plt.grid(color = '0.8')
plt.axis('equal')
plt.scatter(1, 7, color = '#96514d')
plt.scatter(5, 1, color = '#96514d')
plt.scatter(6, 6)
plt.scatter(9, 8)
plt.show()

# グラフをファイルに保存
fig.savefig(save_fig_path)

# 点AC間 の距離

import math

def dist(x1, y1, x2, y2):
    return math.sqrt((x2 - x1)**2 + (y2 - y1)**2)

dat = dist(6, 6, 1, 7)
print('点AC間の距離 = ', dat)

点AC間の距離 =  5.0990195135927845

# 点AD間 の距離

import math

def dist(x1, y1, x2, y2):
    return math.sqrt((x2 - x1)**2 + (y2 - y1)**2)

dat = dist(9, 8, 1, 7)
print('点AD間の距離 = ', dat)

点AD間の距離 =  8.06225774829855

# -*- coding: utf-8 -*-
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
import sympy as sp
import math

# グラフ画像の保存先ファイルパス
save_fig_path = "./data/L006-05_2.png"

fig = plt.figure()
ax = fig.add_subplot(111)

# 中心(9,8)で半径ADの円を描画
circle = plt.Circle((9, 8), 8.06225774829855, ec='#96514d', fill=False)
ax.add_patch(circle)

# 中心(6,6)で半径ACの円を描画
circle = plt.Circle((6, 6), 5.0990195135927845, ec='#96514d', fill=False)
ax.add_patch(circle)

# 2つの点A(1,7)、点B(5,1)を結ぶ線を描画
def func(x1):
    return -x1*3/2 + 17/2

x1 = np.arange(1, 6)
y1 = func(x1)

plt.plot(x1, y1)

# 2つの点の垂直二等分線を描画
def func(x2):
    return 2*x2/3 + 2

x2 = np.arange(3, 10)
y2 = func(x2)

plt.plot(x2, y2)

# 2つの点C(6,6)、点A(1,7)を結ぶ線を描画
def func(x3):
    return -x3/5 + 36/5

x3 = np.arange(1, 7)
y3 = func(x3)

plt.plot(x3, y3)

# 2つの点D(9,8)、点A(1,7)を結ぶ線を描画
def func(x4):
    return x4/8 + 55/8

x4 = np.arange(1, 10)
y4 = func(x4)

plt.plot(x4, y4)

plt.grid(color = '0.8')
plt.axis('equal')
plt.scatter(9, 8, color = '#96514d')
plt.scatter(6, 6, color = '#96514d')
plt.show()

# グラフをファイルに保存
fig.savefig(save_fig_path)

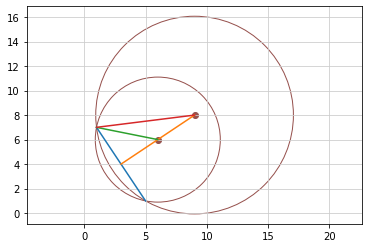
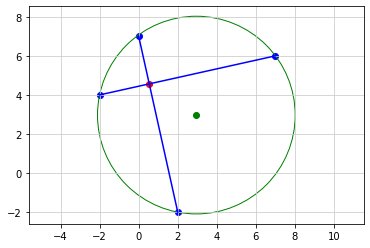
# 点A(-2,4)、点B(2,-2)、点C(7,6) の三点から等距離にある点
# 点A、点B、点C それぞれの間を結ぶと三角形ができる
# 各辺の垂直二等分線を引くと 点P で交わる
# 点P は外心 で 外接円 の中心となる

import math

# グラフ画像の保存先ファイルパス
save_fig_path = "./data/L006-05_3.png"

fig = plt.figure()
ax = fig.add_subplot(111)

# 数式で使う文字の定義
x, y = sp.symbols('x, y')

# 垂直二等分線の式
def perp_bisector(p1, p2):
    ex = ((x-p1[0])**2 + (y-p1[1])**2) - ((p2[0]-x)**2 + (p2[1]-y)**2)
    ex = sp.solve(ex, y)
    return sp.Eq(y, ex[0])

# 2点間の距離
def dist_p2p(p1, p2):
    return math.sqrt((p2[0]-p1[0])**2 + (p2[1]-p1[1])**2)

# ----------

# 3点の座標
x1 = -2; y1= 4
x2 = 2; y2 = -2
x3 = 7; y3 = 6

# 線分AB の垂直二等分線の式
expr1 = perp_bisector((x1, y1), (x2, y2))
display(expr1)

# 線分BC の垂直二等分線の式
expr2 = perp_bisector((x2, y2), (x3, y3))
display(expr2)

# 垂直二等分線の 交点P
p = sp.solve([expr1, expr2])
display(p)

# 点A と 点P との距離
r = dist_p2p((x1, y1), (p[x], p[y]))
display(r)

# 点を描画
plt.scatter(x1, y1, color = 'k')
plt.scatter(x2, y2, color = 'k')
plt.scatter(x3, y3, color = 'k')
plt.scatter(p[x], p[y], color = 'r')

# 円を描画
circle = plt.Circle((p[x], p[y]), r, fill = False, ec = 'r')
ax = plt.gca()
ax.add_patch(circle)

plt.grid(color = '0.8')
plt.axis('equal')
plt.show()

# グラフをファイルに保存
fig.savefig(save_fig_path)

\[\displaystyle y = \frac{2 x}{3} + 1\]

\[\displaystyle y = \frac{77}{16} - \frac{5 x}{8}\]

{x: 183/62, y: 92/31}

5.058065544766189

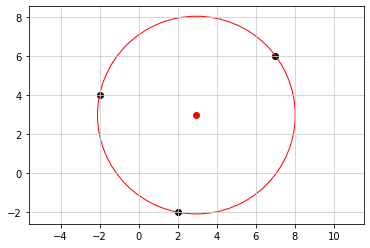
# 点A と 点B とを結ぶ直線の式

# -*- coding: utf-8 -*-
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
import sympy as sp
import math

x = sp.Symbol('x')               # 未知数 x
x1, y1 = sp.symbols('x1, y1')    # 点m の座標
x2, y2 = sp.symbols('x2, y2')    # 点n の座標

y = ((y2 - y1) / (x2 - x1)) * (x - x1) + y1    # 直線の式
y = y.subs({x1:-2, y1:4, x2:7, y2:8})            # 式に値を代入
y

\[\displaystyle \frac{4 x}{9} + \frac{44}{9}\]

# 点A と 点B とを結ぶ直線の式

# -*- coding: utf-8 -*-
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
import sympy as sp
import math

x = sp.Symbol('x')               # 未知数 x
x1, y1 = sp.symbols('x1, y1')    # 点A の座標
x2, y2 = sp.symbols('x2, y2')    # 点B の座標
x3, y3 = sp.symbols('x3, y3')    # 点C の座標

def f(x):
    return  ((y2 - y1) / (x2 - x1)) * (x - x1) + y1

y3 = f(x).subs({x1:7, y1:6, x2:-2, y2:4})
print('y3 = ', y3)

y1 = f(x).subs({x1:-2, y1:4, x2:2, y2:-2})
print('y1 = ', y1)

y2 = f(x).subs({x1:7, y1:6, x2:2, y2:-2})
print('y2 = ', y2)

y3 =  2*x/9 + 40/9
y1 =  1 - 3*x/2
y2 =  8*x/5 - 26/5

# 3点の座標
# x1 = -2; y1= 4
# x2 = 2; y2 = -2
# x3 = 7; y3 = 6

x_1 = np.arange(-2, 3)
y_1 = 1 - 3*x_1/2

plt.plot(x_1, y_1)

x_2 = np.arange(2, 8)
y_2 = 8*x_2/5 - 26/5

plt.plot(x_2, y_2)

x_3 = np.arange(-2, 8)
y_3 = 2*x_3/9 + 40/9

plt.plot(x_3, y_3)

plt.grid(color = '0.8')
plt.axis('equal')
plt.show()

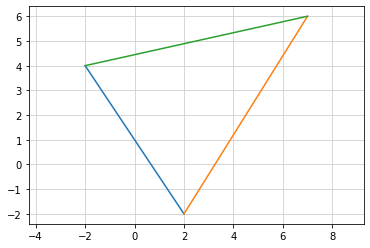
# -*- coding: utf-8 -*-
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
import sympy as sp
import math

# グラフ画像の保存先ファイルパス
save_fig_path = "./data/L006-05_4.png"

fig = plt.figure()
ax = fig.add_subplot(111)

# 数式で使う文字の定義
x, y = sp.symbols('x, y')

# 垂直二等分線の式
def perp_bisector(p1, p2):
    ex = ((x-p1[0])**2 + (y-p1[1])**2) - ((p2[0]-x)**2 + (p2[1]-y)**2)
    ex = sp.solve(ex, y)
    return sp.Eq(y, ex[0])

# 2点間の距離
def dist_p2p(p1, p2):
    return math.sqrt((p2[0]-p1[0])**2 + (p2[1]-p1[1])**2)

# ----------

# 3点の座標
x1 = -2; y1= 4
x2 = 2; y2 = -2
x3 = 7; y3 = 6

# 線分AB の垂直二等分線の式
expr1 = perp_bisector((x1, y1), (x2, y2))

# 線分BC の垂直二等分線の式
expr2 = perp_bisector((x2, y2), (x3, y3))

# 垂直二等分線の 交点P
p = sp.solve([expr1, expr2])

# 点A と 点P との距離
r = dist_p2p((x1, y1), (p[x], p[y]))

# 点を描画
plt.scatter(x1, y1, color = 'k')
plt.scatter(x2, y2, color = 'k')
plt.scatter(x3, y3, color = 'k')
plt.scatter(p[x], p[y], color = 'r')

# 円を描画
circle = plt.Circle((p[x], p[y]), r, fill = False, ec = 'r')
ax = plt.gca()
ax.add_patch(circle)

# 線を描画
x_1 = np.arange(-2, 3)
y_1 = 1 - 3*x_1/2

plt.plot(x_1, y_1)

x_2 = np.arange(2, 8)
y_2 = 8*x_2/5 - 26/5

plt.plot(x_2, y_2)

x_3 = np.arange(-2, 8)
y_3 = 2*x_3/9 + 40/9

plt.plot(x_3, y_3)

plt.grid(color = '0.8')
plt.axis('equal')
plt.show()

# グラフをファイルに保存
fig.savefig(save_fig_path)

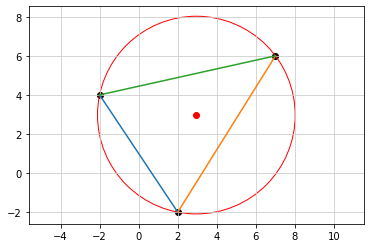
# -*- coding: utf-8 -*-
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
import sympy as sp
import math

# グラフ画像の保存先ファイルパス
save_fig_path = "./data/L006-05_5.png"

fig = plt.figure()
ax = fig.add_subplot(111)

# 数式で使う文字の定義
x, y = sp.symbols('x, y')

# 垂直二等分線の式
def perp_bisector(p1, p2):
    ex = ((x-p1[0])**2 + (y-p1[1])**2) - ((p2[0]-x)**2 + (p2[1]-y)**2)
    ex = sp.solve(ex, y)
    return sp.Eq(y, ex[0])

# 2点間の距離
def dist_p2p(p1, p2):
    return math.sqrt((p2[0]-p1[0])**2 + (p2[1]-p1[1])**2)

# ----------

# 3点の座標
x1 = -2; y1= 4
x2 = 2; y2 = -2
x3 = 7; y3 = 6

# 線分AB の垂直二等分線の式
expr1 = perp_bisector((x1, y1), (x2, y2))

# 線分BC の垂直二等分線の式
expr2 = perp_bisector((x2, y2), (x3, y3))

# 垂直二等分線の 交点P
p = sp.solve([expr1, expr2])

# 点A と 点P との距離
r = dist_p2p((x1, y1), (p[x], p[y]))

# 点を描画
plt.scatter(x1, y1, color = 'k')
plt.scatter(x2, y2, color = 'k')
plt.scatter(x3, y3, color = 'k')
plt.scatter(p[x], p[y], color = 'r')

# 円を描画
circle = plt.Circle((p[x], p[y]), r, fill = False, ec = 'r')
ax = plt.gca()
ax.add_patch(circle)

# 線を描画
x_1 = np.arange(-2, 3)
y_1 = 1 - 3*x_1/2

plt.plot(x_1, y_1, color ='b')

x_2 = np.arange(2, 8)
y_2 = 8*x_2/5 - 26/5

plt.plot(x_2, y_2, color ='b')

x_3 = np.arange(-2, 8)
y_3 = 2*x_3/9 + 40/9

plt.plot(x_3, y_3, color = 'b')

# 垂直二等分線を表示

abx = np.arange(-2, 4)
aby = 2*abx/3 + 1

plt.plot(abx, aby, color = 'y')

bcx = np.arange(3, 9)
bcy = -5*bcx/8 + 77/16

plt.plot(bcx, bcy, color = 'y')

cax = np.arange(1, 4)
cay = -9*cax/2 + 65/4

plt.plot(cax, cay, color = 'y')

plt.grid(color = '0.8')
plt.axis('equal')
plt.show()

# グラフをファイルに保存
fig.savefig(save_fig_path)

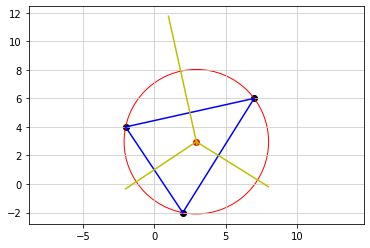
点が4つ以上￥あるとき

• 点と直線の関係

  1. 2点から等距離にある点は複数あり、それを集めると直線になる

  2. 3点から等距離にある点は1つしかない

• 4点から等距離にある点は円の中心となる

• 3点からの場合と同じ

• 5点以上でも同様

# -*- coding: utf-8 -*-
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
import sympy as sp
import math

# グラフ画像の保存先ファイルパス
save_fig_path = "./data/L006-06_1.png"

fig = plt.figure()
ax = fig.add_subplot(111)

# 数式で使う文字の定義
x, y = sp.symbols('x, y')

# 垂直二等分線の式
def perp_bisector(p1, p2):
    ex = ((x-p1[0])**2 + (y-p1[1])**2) - ((p2[0]-x)**2 + (p2[1]-y)**2)
    ex = sp.solve(ex, y)
    return sp.Eq(y, ex[0])

# 2点間の距離
def dist_p2p(p1, p2):
    return math.sqrt((p2[0]-p1[0])**2 + (p2[1]-p1[1])**2)

# ----------

# 4点の座標
x1 = -2; y1= 4
x2 = 2; y2 = -2
x3 = 7; y3 = 6
x4 = 0; y4 = 7

# 線分AB の垂直二等分線の式
expr1 = perp_bisector((x1, y1), (x2, y2))

# 線分BC の垂直二等分線の式
expr2 = perp_bisector((x2, y2), (x3, y3))

# 垂直二等分線の 交点P
p = sp.solve([expr1, expr2])
display(p)

# 点A と 点P との距離
r = dist_p2p((x1, y1), (p[x], p[y]))
display(r)

# 点を描画
plt.scatter(x1, y1, color = 'k')
plt.scatter(x2, y2, color = 'k')
plt.scatter(x3, y3, color = 'k')
plt.scatter(x4, y4, color = 'k')
plt.scatter(p[x], p[y], color = 'r')

# 円を描画
circle = plt.Circle((p[x], p[y]), r, fill = False, ec = 'r')
ax = plt.gca()
ax.add_patch(circle)

plt.grid(color = '0.8')
plt.axis('equal')
plt.show()

# グラフをファイルに保存
fig.savefig(save_fig_path)

{x: 183/62, y: 92/31}

5.058065544766189

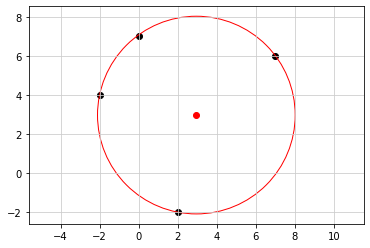
### 方べきの定理 ###

# -*- coding: utf-8 -*-
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
import sympy as sp
import math

# 4点の座標
x1 = -2; y1= 4
x2 = 2; y2 = -2
x3 = 7; y3 = 6
x4 = 0; y4 = 7

x = sp.Symbol('x')               # 未知数 x
x1, y1 = sp.symbols('x1, y1')    # 点m の座標
x2, y2 = sp.symbols('x2, y2')    # 点n の座標

def func(x):
    return ((y2 - y1) / (x2 - x1)) * (x - x1) + y1    # 直線の式

y_a = func(x).subs({x1:-2, y1:4, x2:7, y2:6})
print(y_a)

y_b =  func(x).subs({x1:2, y1:-2, x2:0, y2:7})
print(y_b)

2*x/9 + 40/9
7 - 9*x/2

# グラフ画像の保存先ファイルパス
save_fig_path = "./data/L006-06_2.png"

fig = plt.figure()
ax = fig.add_subplot(111)

# 4点の座標
x1 = -2; y1= 4
x2 = 2; y2 = -2
x3 = 7; y3 = 6
x4 = 0; y4 = 7

# 2つの点A(-2,4)、点C(7,6)を結ぶ線を描画

def func(x1):
    return 2*x1/9 + 40/9

x_1 = np.arange(-2, 8)
y_1 = func(x_1)

plt.plot(x_1, y_1)

# 2つの点B(2,-2)、点D(0,7)を結ぶ線を描画

def func(x2):
    return 7 - 9*x2/2

x_2 = np.arange(0, 3)
y_2 = func(x_2)

plt.plot(x_2, y_2)

# 点を描画
plt.scatter(x1, y1, color = 'k')
plt.scatter(x2, y2, color = 'k')
plt.scatter(x3, y3, color = 'k')
plt.scatter(x4, y4, color = 'k')

plt.grid(color = '0.8')
plt.axis('equal')
plt.show()

# グラフをファイルに保存
fig.savefig(save_fig_path)

# -*- coding: utf-8 -*-
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
import sympy as sp
import math

x = sp.Symbol('x')               # 未知数 x
x1, y1 = sp.symbols('x1, y1')    # 点m の座標
x2, y2 = sp.symbols('x2, y2')    # 点n の座標

def func(x):
    return ((y2 - y1) / (x2 - x1)) * (x - x1) + y1    # 直線の式

y_ab = func(x).subs({x1:-2, y1:4, x2:2, y2:-2})
print(y_ab)

y_bc =  func(x).subs({x1:2, y1:-2, x2:7, y2:6})
print(y_bc)

1 - 3*x/2
8*x/5 - 26/5

y_cd = func(x).subs({x1:7, y1:6, x2:0, y2:7})
print(y_cd)

y_bc =  func(x).subs({x1:0, y1:7, x2:-2, y2:4})
print(y_bc)

7 - x/7
3*x/2 + 7

# グラフ画像の保存先ファイルパス
save_fig_path = "./data/L006-06_3.png"

x = sp.Symbol('x')               # 未知数 x
x1, y1 = sp.symbols('x1, y1')    # 点m の座標
x2, y2 = sp.symbols('x2, y2')    # 点n の座標

# 4点の座標
x1 = -2; y1= 4
x2 = 2; y2 = -2
x3 = 7; y3 = 6
x4 = 0; y4 = 7

fig = plt.figure()
ax = fig.add_subplot(111)

# 数式で使う文字の定義
x, y = sp.symbols('x, y')

# 線分AB の垂直二等分線の式
expr1 = perp_bisector((x1, y1), (x2, y2))

# 線分BC の垂直二等分線の式
expr2 = perp_bisector((x2, y2), (x3, y3))

# 垂直二等分線の 交点P
p = sp.solve([expr1, expr2])

# 2点間の距離
def dist_p2p(p1, p2):
    return math.sqrt((p2[0]-p1[0])**2 + (p2[1]-p1[1])**2)

x_1 = np.arange(-2, 3)
y_1 = 1- 3*x_1/2

plt.plot(x_1, y_1, color = 'r')

x_2 = np.arange(2, 8)
y_2 = 8*x_2/5 - 26/5

plt.plot(x_2, y_2, color = 'r')

x_3 = np.arange(0, 8)
y_3 = 7 - x_3/7

plt.plot(x_3, y_3, color = 'r')

x_4 = np.arange(-2, 1)
y_4 = 3*x_4/2 + 7

plt.plot(x_4, y_4, color = 'r')

# 点A と 点P との距離
r = dist_p2p((x1, y1), (p[x], p[y]))

# 点を描画
plt.scatter(x1, y1, color = 'b')
plt.scatter(x2, y2, color = 'b')
plt.scatter(x3, y3, color = 'b')
plt.scatter(x4, y4, color = 'b')
plt.scatter(p[x], p[y], color = 'r')

# 円を描画
circle = plt.Circle((p[x], p[y]), r, fill = False, ec = 'g')
ax = plt.gca()
ax.add_patch(circle)

plt.grid(color = '0.8')
plt.axis('equal')
plt.show()

# グラフをファイルに保存
fig.savefig(save_fig_path)

# -*- coding: utf-8 -*-
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
import sympy as sp
import math

# グラフ画像の保存先ファイルパス
save_fig_path = "./data/L006-06_4.png"

fig = plt.figure()
ax = fig.add_subplot(111)

x = sp.Symbol('x')               # 未知数 x
x1, y1 = sp.symbols('x1, y1')    # 点m の座標
x2, y2 = sp.symbols('x2, y2')    # 点n の座標

# 4点の座標
x1 = -2; y1= 4
x2 = 2; y2 = -2
x3 = 7; y3 = 6
x4 = 0; y4 = 7

# 数式で使う文字の定義
x, y = sp.symbols('x, y')

# 垂直二等分線の式
def perp_bisector(p1, p2):
    ex = ((x-p1[0])**2 + (y-p1[1])**2) - ((p2[0]-x)**2 + (p2[1]-y)**2)
    ex = sp.solve(ex, y)
    return sp.Eq(y, ex[0])

# 2点間の距離
def dist_p2p(p1, p2):
    return math.sqrt((p2[0]-p1[0])**2 + (p2[1]-p1[1])**2)

# 線分AB の垂直二等分線の式
expr1 = perp_bisector((x1, y1), (x2, y2))

# 線分BC の垂直二等分線の式
expr2 = perp_bisector((x2, y2), (x3, y3))

# 垂直二等分線の 交点P
p = sp.solve([expr1, expr2])

x_1 = np.arange(-2, 3)
y_1 = 1- 3*x_1/2

plt.plot(x_1, y_1, color = 'r')

x_2 = np.arange(2, 8)
y_2 = 8*x_2/5 - 26/5

plt.plot(x_2, y_2, color = 'r')

x_3 = np.arange(0, 8)
y_3 = 7 - x_3/7

plt.plot(x_3, y_3, color = 'r')

x_4 = np.arange(-2, 1)
y_4 = 3*x_4/2 + 7

plt.plot(x_4, y_4, color = 'r')

# 点A と 点P との距離
r = dist_p2p((x1, y1), (p[x], p[y]))

# 2つの点A(-2,4)、点C(7,6)を結ぶ線を描画

def func(x1):
    return 2*x1/9 + 40/9

x_1 = np.arange(-2, 8)
y_1 = func(x_1)

plt.plot(x_1, y_1, color = 'b')

# 2つの点B(2,-2)、点D(0,7)を結ぶ線を描画

def func(x2):
    return 7 - 9*x2/2

x_2 = np.arange(0, 3)
y_2 = func(x_2)

plt.plot(x_2, y_2, color = 'b')

# 点を描画
plt.scatter(x1, y1, color = 'b')
plt.scatter(x2, y2, color = 'b')
plt.scatter(x3, y3, color = 'b')
plt.scatter(x4, y4, color = 'b')
plt.scatter(p[x], p[y], color = 'r')

# 円を描画
circle = plt.Circle((p[x], p[y]), r, fill = False, ec = 'g')
ax = plt.gca()
ax.add_patch(circle)

plt.grid(color = '0.8')
plt.axis('equal')
plt.show()

# グラフをファイルに保存
fig.savefig(save_fig_path)

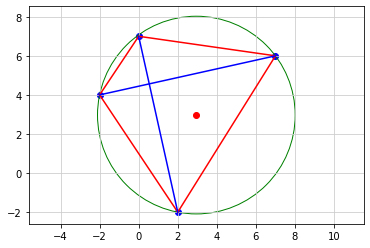
### 方べきの定理 ###

# -*- coding: utf-8 -*-
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
import sympy as sp
import math

# 4点の座標
x1 = -2; y1= 4
x2 = 2; y2 = -2
x3 = 7; y3 = 6
x4 = 0; y4 = 7

x = sp.Symbol('x')               # 未知数 x
y = sp.Symbol('y')               # 未知数 Y
x1, y1 = sp.symbols('x1, y1')    # 点m の座標
x2, y2 = sp.symbols('x2, y2')    # 点n の座標

def func(x):
    return ((y2 - y1) / (x2 - x1)) * (x - x1) + y1    # 直線の式

y_a = func(x).subs({x1:-2, y1:4, x2:7, y2:6})
print(y_a)

y_b =  func(x).subs({x1:2, y1:-2, x2:0, y2:7})
print(y_b)

x = sp.Symbol('x')


ty = sp.Eq(y, y_a)
jy = sp.Eq(y, y_b)

ans = sp.solve([ty, jy])
ans

2*x/9 + 40/9
7 - 9*x/2

{x: 46/85, y: 388/85}

# グラフ画像の保存先ファイルパス
save_fig_path = "./data/L006-06_5.png"

# 2つの点A(-2,4)、点C(7,6)を結ぶ線を描画

fig = plt.figure()
ax = fig.add_subplot(111)

# 4点の座標
x1 = -2; y1= 4
x2 = 2; y2 = -2
x3 = 7; y3 = 6
x4 = 0; y4 = 7

# 2つの点A(-2,4)、点C(7,6)を結ぶ線を描画

def func(x1):
    return 2*x1/9 + 40/9

x_1 = np.arange(-2, 8)
y_1 = func(x_1)

plt.plot(x_1, y_1)

# 2つの点B(2,-2)、点D(0,7)を結ぶ線を描画

def func(x2):
    return 7 - 9*x2/2

x_2 = np.arange(0, 3)
y_2 = func(x_2)

plt.plot(x_2, y_2)

x = 46/85
y = 388/85

# 点を描画
plt.scatter(x1, y1, color = 'k')
plt.scatter(x2, y2, color = 'k')
plt.scatter(x3, y3, color = 'k')
plt.scatter(x4, y4, color = 'k')
plt.scatter(x, y, color = 'r')

plt.grid(color = '0.8')
plt.axis('equal')
plt.show()

# グラフをファイルに保存
fig.savefig(save_fig_path)

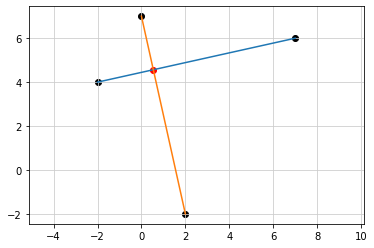
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
import sympy as sp
import math

x = sp.Symbol('x')               # 未知数 x
x1, y1 = sp.symbols('x1, y1')    # 点m の座標
x2, y2 = sp.symbols('x2, y2')    # 点n の座標

# 4点の座標
x1 = -2; y1= 4
x2 = 2; y2 = -2
x3 = 7; y3 = 6
x4 = 0; y4 = 7

# 交点の座標
x = 46/85; y = 388/85

# 点AX間 の距離

def dist(x1, y1, x2, y2):
    return math.sqrt((x2 - x1)**2 + (y2 - y1)**2)

a = dist(x1, y1, x, y)
print('点AX間の距離 = ', a)

d = dist(x2, y2, x, y)
print('点BX間の距離 = ', d)

b = dist(x3, y3, x, y)
print('点CX間の距離 = ', b)

c = dist(x4, y4, x, y)
print('点DX間の距離 = ', c)

ab = a * b
cd = c * d

print(ab, cd)

点AX間の距離 =  2.603165493823874
点BX間の距離 =  6.724844192378341
点CX間の距離 =  6.616378963469014
点DX間の距離 =  2.494700264914546
17.22352941176471 16.776470588235295

# -*- coding: utf-8 -*-
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
import sympy as sp
import math

# グラフ画像の保存先ファイルパス
save_fig_path = "./data/L006-06_6.png"

fig = plt.figure()
ax = fig.add_subplot(111)

x = sp.Symbol('x')               # 未知数 x
x1, y1 = sp.symbols('x1, y1')    # 点m の座標
x2, y2 = sp.symbols('x2, y2')    # 点n の座標

# 4点の座標
x1 = -2; y1= 4
x2 = 2; y2 = -2
x3 = 7; y3 = 6
x4 = 0; y4 = 7

# 数式で使う文字の定義
x, y = sp.symbols('x, y')

# 垂直二等分線の式
def perp_bisector(p1, p2):
    ex = ((x-p1[0])**2 + (y-p1[1])**2) - ((p2[0]-x)**2 + (p2[1]-y)**2)
    ex = sp.solve(ex, y)
    return sp.Eq(y, ex[0])

# 2点間の距離
def dist_p2p(p1, p2):
    return math.sqrt((p2[0]-p1[0])**2 + (p2[1]-p1[1])**2)

# 線分AB の垂直二等分線の式
expr1 = perp_bisector((x1, y1), (x2, y2))

# 線分BC の垂直二等分線の式
expr2 = perp_bisector((x2, y2), (x3, y3))

# 垂直二等分線の 交点P
p = sp.solve([expr1, expr2])


# 点A と 点P との距離
r = dist_p2p((x1, y1), (p[x], p[y]))

# 2つの点A(-2,4)、点C(7,6)を結ぶ線を描画

def func(x1):
    return 2*x1/9 + 40/9

x_1 = np.arange(-2, 8)
y_1 = func(x_1)

plt.plot(x_1, y_1, color = 'b')

# 2つの点B(2,-2)、点D(0,7)を結ぶ線を描画

def func(x2):
    return 7 - 9*x2/2

x_2 = np.arange(0, 3)
y_2 = func(x_2)

plt.plot(x_2, y_2, color = 'b')

# 交点の座標
cx = 46/85; cy = 388/85

# 点を描画
plt.scatter(x1, y1, color = 'b')
plt.scatter(x2, y2, color = 'b')
plt.scatter(x3, y3, color = 'b')
plt.scatter(x4, y4, color = 'b')
plt.scatter(p[x], p[y], color = 'g')
plt.scatter(cx, cy, color = 'r')

# 円を描画
circle = plt.Circle((p[x], p[y]), r, fill = False, ec = 'g')
ax = plt.gca()
ax.add_patch(circle)

plt.grid(color = '0.8')
plt.axis('equal')
plt.show()

# グラフをファイルに保存
fig.savefig(save_fig_path)