5 点と直線の距離¶
ピタゴラスの定理¶
直角三角形の斜辺の長さの2乗は、残りの2辺の長さを2乗して足したものに等しい
斜辺の長さを c、他の2辺の長さを a、b とすると
$ c^2 = a^2 + b^2$
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import sympy as sp
c = sp.Symbol('c')
a, b = sp.symbols('a, b')
expr = sp.Eq(c **2, a **2 + b ** 2)
display(expr)
2点間の距離¶
線分AB の 距離c を求めるには ピタゴラスの定理 を利用する
点A(x1, y1)、点B(x2, y2) を結ぶ 直線の距離ab を求めるには
点A を通る x軸 に平行な直線と 点B を通る y軸 に平行な直線を引く
2つの直線は 点C(x2, y1) で直交する
点AC の距離は \(a = x2 - x1\)
点BC の距離は \(b = y2 - y1\)
ピタゴラスの定理から 線分AB の長さは
\(c^2 = (x2-x1)^2+(y2-y1)^2\)
c = sp.Symbol('c')
x1, x2, y1, y2 = sp.symbols('x1, x2, y1, y2')
expr = sp.Eq(c ** 2, (x2 - x1) ** 2 + (y2 - y1) ** 2)
display(expr)
expr = sp.Eq(c , sp.sqrt((x2 - x1) ** 2 + (y2 - y1) ** 2))
display(expr)
2点間の距離を求める関数を定義する
平方根の計算には Mathモジュール に含まれる sqrt() を使う
import math
def dist(x1, y1, x2, y2):
return math.sqrt((x2 - x1)**2 + (y2 - y1)**2)
dat = dist(-2, -3, 6, 2)
print('点AB間の距離 = ', dat)
点AB間の距離 = 9.433981132056603
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import sympy as sp
x1 = -2
y1 = -3
x2 = 6
y2 = 2
a = (y2 - y1) / (x2 - x1)
b = -(a * (x1 + x2) - (y1 + y2)) / 2
x = np.arange(x1, x2 + 1)
y = a * x + b
plt.plot(x, y)
plt.axis('equal')
plt.grid(color = '0.8')
plt.scatter(x1, y1, color = 'g')
plt.scatter(x2, y2, color = 'g')
plt.show()
原点と直線との距離¶
点と直線との距離は点から直線に下ろした垂線の長さ と定義されている
\(y=-2 \times x + 5\) と 原点の距離
垂線の傾きは \(a1 \times a2 = -1\) より \(\dfrac{1}{2}\)
垂線は $y = 1/2 * x
import sympy as sp
sp.init_printing()
# 記号と式を定義
x, y = sp.symbols('x, y')
expr01 = sp.Eq(y, -2 * x + 5)
expr02 = sp.Eq(y, 1/2 * x)
# 連立方程式を解く
p = sp.solve([expr01, expr02])
p
# 原点と直線の垂線を描く
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
def func01(x):
return -2 * x + 5
def func02(x):
return 1/2 * x
x1 = np.arange(-1, 4)
x2 = np.arange(0, 3)
y1 = func01(x1)
plt.plot(x1, y1)
y2 = func02(x2)
plt.plot(x2, y2)
plt.axis('equal')
plt.grid(color = '0.8')
plt.scatter(2, 1, color = 'r')
plt.show()
# 原点と直線の距離を求める
import math
def dist_p2p(p1, p2):
return math.sqrt((p2[0] - p1[0])**2 + (p2[1] - p1[1])**2)
d = dist_p2p((0, 0), (p[x], p[y]))
d
原点と直線との距離¶
点と直線との距離は点から直線に下ろした垂線の長さ と定義されている
\(y=-2 \times x + 5\) と 原点の距離
垂線の傾きは \(a1 \times a2 = -1\) より \(\dfrac{1}{2}\)
垂線は $y = 1/2 * x
import sympy as sp
sp.init_printing()
# 記号と式を定義
x, y = sp.symbols('x, y')
expr01 = sp.Eq(y, -2 * x + 5)
expr02 = sp.Eq(y, 1/2 * x)
# 連立方程式を解く
p = sp.solve([expr01, expr02])
p
# 原点と直線の垂線を描く
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
def func01(x):
return -2 * x + 5
def func02(x):
return 1/2 * x
x1 = np.arange(-1, 4)
x2 = np.arange(0, 3)
y1 = func01(x1)
plt.plot(x1, y1)
y2 = func02(x2)
plt.plot(x2, y2)
plt.axis('equal')
plt.grid(color = '0.8')
plt.scatter(2, 1, color = 'r')
plt.show()
# 原点と直線の距離を求める
import math
def dist_p2p(p1, p2):
return math.sqrt((p2[0] - p1[0])**2 + (p2[1] - p1[1])**2)
d = dist_p2p((0, 0), (p[x], p[y]))
d
点と直線の距離¶
import numpy as np
import sympy as sp
import math
sp.init_printing()
# 垂線の式
x = sp.Symbol('x')
ex = - 3/2 * (x - 1) + 6
display(ex)
# 2直線の交点
y = sp.Symbol('y')
expr1 = sp.Eq(y, 2/3 * x + 1)
expr2 = sp.Eq(y, ex)
p = sp.solve([expr1, expr2])
display(p)
# 点と直線の距離
def dist_p2p(p1, p2):
return math.sqrt((p2[0] - p1[0])**2 + (p2[1] - p1[1])**2)
d = dist_p2p((1, 6), (p[x], p[y]))
d
点と直線の距離の公式¶
点と直線の距離は、与えられた点から直線に下ろした垂線の足の座標がわかれば求められる
直線の式は \(ly = ax + b\) だけでなく \(\quad ax + by + c = 0 (a \neq 0 または b \neq 0)\) であらわせる
直線と点(x1, y1)の距離を d とすると \(\quad d = \dfrac{|a \times x1 + b \times y1 + c|}{\sqrt{(a^2 + b^2)}}\) \(\quad \dfrac {2}{3} \times x - y + 1 = 0 \quad (y = \dfrac{2}{3} \times x + 1)\)
#%matplotlib inline
#import matplotlib.pyplot as plt
import numpy as np
import sympy as sp
import math
def dist_p2p(p, a, b, c):
return math.fabs(a * p[0] + b * p[1] + c) / math.sqrt(a**2 +b**2)
d = dist_p2p((1, 6), 2/3, -1, 1)
d
3.605551275463989
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import sympy as sp
import math
def func01(x):
return 2/3 * x + 1
def func02(x):
return -3/2 * x + 7.5
x1 = np.arange(-5, 10)
x2 = np.arange(1, 4)
y1 = func01(x1)
plt.plot(x1, y1)
y2 = func02(x2)
plt.plot(x2, y2)
plt.axis('equal')
plt.grid(color = '0.8')
plt.scatter(1, 6, color = 'r')
plt.show()
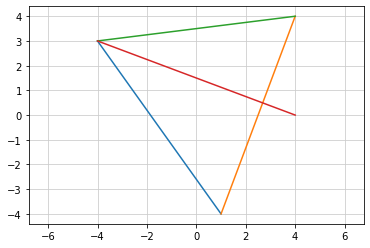
三角形の面積¶
点A(-4,3)、点B(1,-4)、点C(4,4)を頂点とする三角形ABCの面積
辺BCを底辺lとし、点Aから辺BCに下ろした垂線の足までの長さを高さhとする
底辺(l) × 高さ(h) × 1/2 で三角形の面積が求められる
import numpy as np
import sympy as sp
import math
# 2点間の距離を求める関数
def dist_p2p(p1, p2):
return math.sqrt((p2[0] - p1[0])**2 + (p2[1] - p1[1])**2)
# 点と直線の距離の公式
def dist_p2l(p, a, b, c):
return math.fabs(a * p[0] + b * p[1] + c) / math.sqrt(a**2 +b**2)
# 式で使う記号を定義
a, b = sp.symbols('a, b') # 傾きa, 切片b
x = sp.symbols('x') # 未知数x
# 辺BC の長さ
l = dist_p2p((1, -4), (4, 4))
print('辺BCの長さ = ', l)
# 辺BC の直線の式
ex1 = sp.Eq(-4, a*1 + b)
ex2 = sp.Eq(4, a*4 + b)
ans = sp.solve([ex1, ex2])
display('辺BCの式', ans[a]*x + ans[b])
# 点A と 辺BC の距離
h = dist_p2l((-4, 3), ans[a], -1, ans[b])
print('三角形ABCの高さ = ', h)
# 三角形の面積
s = 1/2 * l * h
print('三角形ABDの面積 = ', s)
辺BCの長さ = 8.54400374531753
'辺BCの式'
三角形ABCの高さ = 7.139509978963964
三角形ABDの面積 = 30.499999999999996
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import sympy as sp
import math
# 点と直線の距離の公式
def dist_p2l(p, a, b, c):
return math.fabs(a * p[0] + b * p[1] + c) / math.sqrt(a**2 +b**2)
# 式で使う記号を定義
a, b = sp.symbols('a, b') # 傾きa, 切片b
x = sp.symbols('x') # 未知数x
# 辺AB の直線の式
ex1 = sp.Eq(3, a*-4 + b)
ex2 = sp.Eq(-4, a*1 + b)
ans = sp.solve([ex1, ex2])
display('辺ABの式', ans[a]*x + ans[b])
# 辺BC の直線の式
ex1 = sp.Eq(-4, a*1 + b)
ex2 = sp.Eq(4, a*4 + b)
ans = sp.solve([ex1, ex2])
display('辺BCの式', ans[a]*x + ans[b])
# 辺CA の直線の式
ex1 = sp.Eq(4, a*4 + b)
ex2 = sp.Eq(3, a*-4 + b)
ans = sp.solve([ex1, ex2])
display('辺CAの式', ans[a]*x + ans[b])
# 垂線の式
x = sp.Symbol('x')
ex = - 3/8 * (x + 4) + 3
display('垂線の式',ex)
'辺ABの式'
'辺BCの式'
'辺CAの式'
'垂線の式'
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import sympy as sp
import math
def func01(x):
return -7*x/5 - 13/5
def func02(x):
return 8*x/3 - 20/3
def func03(x):
return x/8 + 7/2
def func04(x):
return 1.5-0.375*x
x1 = np.arange(-4, 2)
x2 = np.arange(1, 5)
x3 = np.arange(-4, 5)
x4 = np.arange(-4, 5)
y1 = func01(x1)
plt.plot(x1, y1)
y2 = func02(x2)
plt.plot(x2, y2)
y3 = func03(x3)
plt.plot(x3,y3)
y4 = func04(x4)
plt.plot(x4,y4)
plt.axis('equal')
plt.grid(color = '0.8')
plt.show()
# 垂線の式
x = sp.Symbol('x')
ex = - 3/2 * (x - 1) + 6
display(ex)
# 2直線の交点
y = sp.Symbol('y')
expr1 = sp.Eq(y, 2/3 * x + 1)
expr2 = sp.Eq(y, ex)
p = sp.solve([expr1, expr2])
display(p)
{x: 3.00000000000000, y: 3.00000000000000}
点と直線との距離の公式の導き方¶
点と直線との距離を求めるには公式を利用するのが簡単で確実
文字式を用いるのは直線の傾きや点の位置にかかわらずどんな場合でも使えるから
点A(x1,y1) と 直線A との距離を求めるには、まず点Aが原点に来るようにする
点A が原点に移動した場合の 直線B の式 \(\quad x + b \times y + c = 0 ... ①\)
直線の傾きがわかるように式を変形する \(\quad y = -\dfrac{a}{b} \times x - \dfrac{c}{b} ... ①'\)
点A から 直線B に下ろした垂線の式 \(\quad y = \dfrac{b}{a} \times x ... ②\)
② を ① に代入して x座標 を求める \(\quad a \times x + b \times (\dfrac{b}{a} \times x) + c = 0\)\(\quad x = - a \times \dfrac{c}{a^2 + b^2} ... ③\)
③ を ② に代入して y座標 を求める \(\quad y = \dfrac{b}{a} \times (-a \times \dfrac{c}{a^2+b^2}) = -b \times \dfrac{c}{a^2+b^2} ... ④\)
求めた点と原点との距離 \(\quad d = \sqrt{(-a \times \dfrac{c}{a^2 + b^2})^2 + (-b \times \dfrac{c}{a^2 + b^2})^2}\) \(\quad d = \sqrt{(\dfrac{c^2}{a^2 + b^2}}\) \(\quad d = \dfrac{|c|}{\sqrt{a^2 + b^2}} ... ⑤\)
点A が原点から移動した場合の 直線A の式
x方向の移動量は -x1
y方向の移動量は -y1
直線B が y軸 と交わる 点D(0,-c/b) に足すと \((-x1,(-\frac{c}{b})-y1)\) \(\quad y = a(x - x1) + y1\) に代入すると \(\quad y = -a/b \times (x - (-x1)) + (-\dfrac{c}{b} - y1)\)
右辺が 0 となるように整理すると \(\quad a \times x + b \times y + (a \times x1 + b \times y1 + c)... ⑥\)
点(x1,y1) と 直線A との距離
式⑥ の \((a \times x1 + b \times y1 + c)\) が定数となる
式⑤ に代入すると \(\quad d = \dfrac{|a \times x1 + b \times y1 + c|} {\sqrt{a^2 + b^2}} ... ⑦\)
点と直線の公式 ⑦ になる
import numpy as np
import sympy as sp
import math
a, b, c = sp.symbols('a, b, c')
x = sp.Symbol('x')
px = sp.solve(a*x + b*(b/a*x) + c, x)
display(px[0])
py = b/a * px[0]
display(py)
d = sp.sqrt((px[0]**2) + (py**2))
display(d)
\display(sp.simplify(d))