3 直線の式の求め方¶
方程式を解く¶
関数と方程式¶
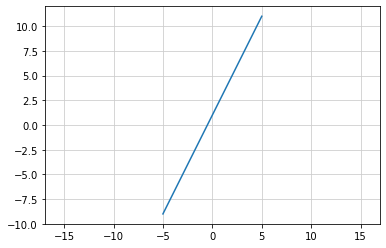
関数 y = 2x + 1 のグラフ
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
# 関数 y = 2x + 1
def func_line(x):
return 2 * x + 1
# y = 2x + 1 のプロッティング
x = np.arange(-5, 6)
y = func_line(x)
plt.plot(x, y)
# 表示
plt.grid(color = '0.8')
plt.axis('equal')
plt.show()
# x値 が決まれば y値が一意に決まる
# 未知数を左辺に移項すると
# 2x - y = 1 という方程式になる
# 方程式の解の集まりが y = 2x + 1 のグラフとなる
直線の方程式¶
直線の方程式の表し方
y = ax + b … ①
ax + by + c = 0 (a ≠ 0 または b ≠ 0) … ②
式① では y軸 に平行な直線を表せない
式② では a = 0 のときには x軸 に平行な直線、b = 0 の時には y軸 に平行な直線となる
式② は平面上のすべての直線を表すことができる
y = (a/b)x - (c/b) … a ≠ 0 または b ≠ 0
y = (a / b) * x + (c / b) のグラフ化
a, b, c の値を入力(b ≠ 0 … b = 0 とするとエラーになる
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
def func_g(x):
return (a * x) / b + c / b
print('y = (a / b) * x + (c / b) のグラフ化')
print('a, b, c の値を入力(b ≠ 0 ... b = 0 とするとエラーになる)')
a = float(input('a = '))
b = float(input('b = '))
c = float(input('c = '))
x = np.arange(-5, 6)
y = func_g(x)
plt.plot(x, y)
plt.grid(color = '0.8')
plt.axis('equal')
plt.show()
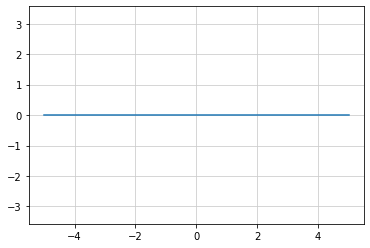
y = (a / b) * x + (c / b) のグラフ化
a, b, c の値を入力(b ≠ 0 ... b = 0 とするとエラーになる)
a = 0
b = 1
c = 0
y = (a * x + c) / b のグラフ化
a, b, c の値を入力(b ≠ 0)
∵ b = 0 とするとエラーになる
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
def func_g(x):
return (a * x + c ) / b
print('y = (a * x + c) / b のグラフ化')
print('a, b, c の値を入力(b ≠ 0 ... b = 0 とするとエラーになる)')
a = float(input('a = '))
b = float(input('b = '))
c = float(input('c = '))
x = np.arange(-5, 6)
y = func_g(x)
plt.plot(x, y)
plt.grid(color = '0.8')
plt.show()
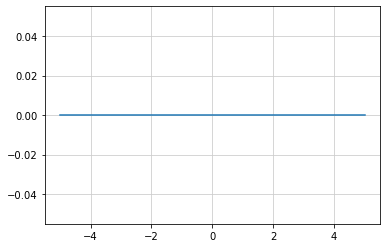
y = (a * x + c) / b のグラフ化
a, b, c の値を入力(b ≠ 0 ... b = 0 とするとエラーになる)
a = 0
b = 5
c = 0
y = (a * x + c) / b のグラフ化
a, b, c の値を入力(a ≠ 0 もしくは b ≠ 0)
※ a = 0 の時は x軸に平行な直線
※ b = 0 の時は y軸に平行な直線
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
def func_g(x):
return (a * x + c ) / b
print('y = (a * x + c) / b のグラフ化')
print('a, b, c の値を入力(a ≠ 0 もしくは b ≠ 0)')
print('※ a = 0 の時は x軸に平行な直線')
print('※ b = 0 の時は y軸に平行な直線')
a = float(input('a = '))
b = float(input('b = '))
c = float(input('c = '))
if b != 0:
x = np.arange(-5, 6)
y = func_g(x)
else:
x =[a, a]
y =[-c, c]
plt.plot(x, y)
plt.grid(color = '0.8')
plt.show()
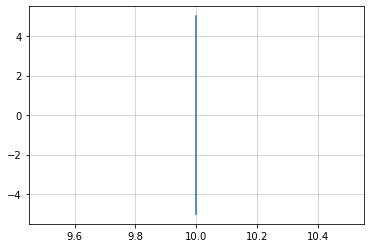
y = (a * x + c) / b のグラフ化
a, b, c の値を入力(a ≠ 0 もしくは b ≠ 0)
※ a = 0 の時は x軸に平行な直線
※ b = 0 の時は y軸に平行な直線
a = 10
b = 0
c = 5
方程式とグラフ¶
太郎君の家から公園までの距離は2100m
毎分70mの歩速で出かけた
家を出てからの時間を x(分)
公園までの残りの距離を y(m)
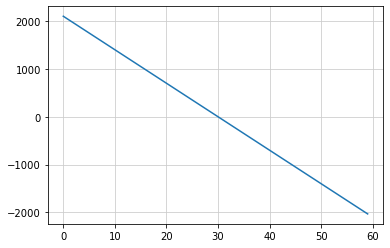
y を求める方程式: y = 2100 - 70x
y = 2100 - 70x のグラフを描く
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
def func(x):
return 2100 - 70 * x
x = np.arange(0, 60)
y = func(x)
plt.plot(x, y)
plt.grid(color = '0.8')
plt.show()
SymPy で計算する¶
式を定義する¶
複雑な方程式は代数計算用の SymPyモジュール を利用する
import sympy as sp
x = sp.Symbol('x') # 記号を定義
y = 2100 - 70 * x
y # 式を表示
値を代入する¶
ans = y.subs(x, 10)
ans
import sympy as sp
x = sp.Symbol('x')
y = 2100 - 70 * x
print(y)
display(y)
ans = y.subs(x, 10)
print(ans)
display(ans)
2100 - 70*x
1400
複数の文字を含んだ式¶
半径 r の円の面積は πr**2 で求められる
円周率 π は SymPyモジュール に’pi’として定義されている
プログラムで定義するのは r の値だけ
r = sp.Symbol('r')
expr = sp.pi * r ** 2
display(expr)
半径が 5 の円の面積を求めるには subs() の引数を ディクショナリ型で指定する
円周率は 3.14
y = expr.subs({sp.pi: 3.14, r: 5})
display(y)
y = expr.subs({sp.pi: float(sp.pi), r: 5})
display(y)
※ 円周率を float(sp.pi) とすると、π の値が 3.141592653589793 となる
(x, y) を通って傾きが a の直線の式¶
切片 b の求め方¶
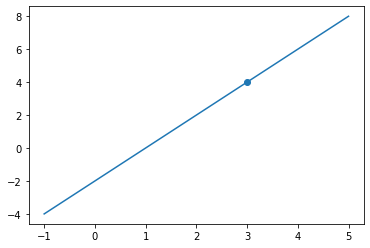
直線をあらわす式は y = 2x - 2
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
def func(x):
return 2 * x - 2
x = np.arange( -1, 6)
y = func(x)
plt.plot(x, y)
plt.scatter(3, 4)
plt.show
<function matplotlib.pyplot.show(close=None, block=None)>
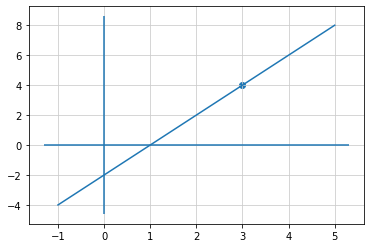
座標軸を描画する
グラフを見やすくするためにグリッド/x軸/y軸を描画する
plt.hlines() で x軸 を描画
plt.hlines() で y軸 を描画
plt.axis() で座標軸の範囲を取得
plt.plot(x, y) # グラフを描画
plt.scatter(3, 4) # (3, 4)に点を描画
xmin, xmax, ymin, ymax = plt.axis() # 座標軸の範囲を取得
plt.hlines(0, xmin, xmax) # x軸 を描画
plt.vlines(0, ymin, ymax) # y軸 を描画
plt.grid(color = '0.8') # グリッドを表示
plt.show()
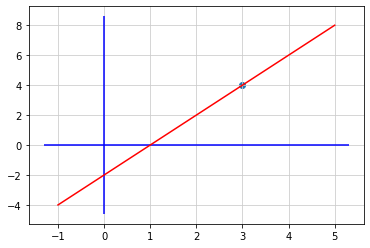
線分の色を指定
color = ‘…’ で線分の色を指定
色の種類は 略号 ‘r’(赤)、‘g’(緑)、‘b’(青)などや、rgb値 ’#rrggbb’で指定できる
plt.plot(x, y, color = 'r')
plt.scatter(3, 4)
xmin, xmax, ymin, ymax = plt.axis()
plt.hlines(0, xmin, xmax, color = 'b')
plt.vlines(0, ymin, ymax, color = 'b')
plt.grid(color = '0.8')
plt.show()
公式を利用する¶
平面上の直線の式は
y = ax + b … ①
点A の座礁(x1,y1)を代入すると
y1 = ax1 + b … ②
① と ② の式から b を消すために ① - ② を計算する
y - y1 = ax + b - (ax1 + b)
y - y1 = ax + b - ax1 - b
y - y1 = a(x - x1)
y = a(x - x1) + y1 … 点A を通る傾き a の直線
点A を(3, 4)とし、傾きを 2 とすると
y = 2x - 2
SymPy を使って計算する¶
y = a(x - x1) + y1
SymPy を使って傾きが 2 で、点(3, 4)を通る直線の式を求める
import sympy as sp
x = sp.Symbol('x') # 未知数 x
a = sp.Symbol('a') # 傾き a
x1, y1 = sp.symbols('x1, y1') # 直線上の点(x1, y1)
y = a * (x - x1) + y1
y = y.subs({a: 2, x1: 3, y1: 4 })
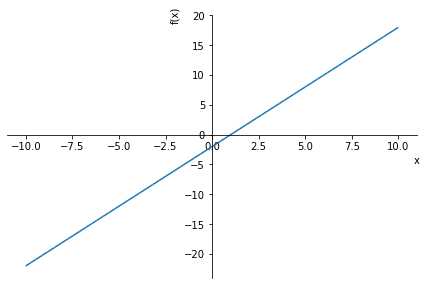
y
sp.plot(y)
<sympy.plotting.plot.Plot at 0x18e67d1da00>
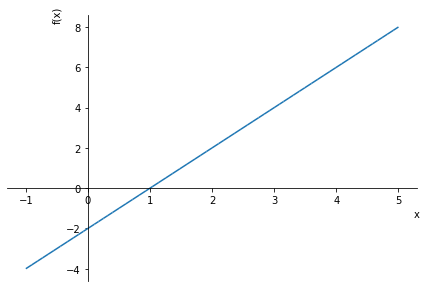
sp.plot(y, (x, -1, 5))
<sympy.plotting.plot.Plot at 0x18e69616970>
2点を通る直線の式¶
直線の傾きを求める¶
2点を通る直線は1本だけとなる
2つの座標から y = ax + b の式を求める
点m の座標を (x1, y1)、点n の座標を(x2, y2)とする
直線の傾き a は (y2 - y1) / (x2 - x1)
点m の値と傾きが与えられた式 y = a (x - x1) + y1 に代入すると
y = ((y2 - y1) / (x2 - x1))(x - x1) + y1 (x1 ≠ x2)
点m(1, 0)、点n(3, 4) の場合、SymPyを使って計算すると
import sympy as sp
x = sp.Symbol('x') # 未知数 x
x1, y1 = sp.symbols('x1, y1') # 点m の座標
x2, y2 = sp.symbols('x2, y2') # 点n の座標
y = ((y2 - y1) / (x2 - x1)) * (x - x1) + y1 # 直線の式
y = y.subs({x1:1, y1:0, x2:3, y2:4}) # 式に値を代入
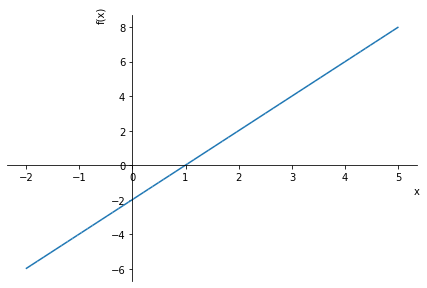
y
sp.plot(y, (x, -2, 5))
<sympy.plotting.plot.Plot at 0x181a2027df0>
連立方程式を使って2点を通る直線の式を求める¶
点m(x1, y1) を通る傾き a の直線
y1 = a * x1 + b
点n(x2, y2) を通る傾き a の直線
y2 = a * y2 + b
点m、点n を通る直線を求めると
y2 - y1 = a * (x2 - x1)
点m(1, 0)、点n(3, 4) を代入すると
4 = a * 2
a = 2
求められた a の値を 点m(1, 0) の値と共に y1 = a * x1 + b の式に代入すると
0 = 2 * 1 + b
b = 2
点m(1, 0)、点n(3, 4) を通る直線の式は
y = 2 * a + 2
a = sp.Symbol('a') # 直線の傾き a
b = sp.Symbol('b') # 直線の切片 b
expr1 = a + b # 0 = a + b
expr2 = 3 * a + b - 4 # 0 = 3 * a + b - 4
ans1 = sp.solve([expr1, expr2]) # 連立方程式を解く
print(ans1)
# solve() を使って方程式を解くときは左辺(または右辺)が 0(ゼロ) になるように式を整理してから定義する
# 式の整理を行わない場合は SymPy の Eq() を使って式を定義する
expr1 = sp.Eq(0, a + b) # 0 = a + b
expr2 = sp.Eq(4, 3 * a + b) # 4 = 3 * a + b
ans2 = sp.solve([expr1, expr2])
print(ans2)
{a: 2, b: -2}
{a: 2, b: -2}
二直線の交点¶
平面上にある2本の直線は、平行でなければ必ず平面上の1点(交点)で交わる
直線は直線の方程式で表すことができる
2本の直線の交点は連立方程式の解として求められる
- 太郎クンは自宅から買い物に出かけました。次郎クンは太郎君を追って 6分
あとから自宅を出ました。
太郎クンは分速70mの速さで歩いています。次郎クンは分速100mの速さで掛け出しました。
太郎クンが進む距離は x分間 には 70 * x(m)、次郎クンは 100 * x(m)
2人の距離が縮まるのは 1分間 に 30(m)
次郎クンが自宅を出たときの太郎クンの位置は 70 * 6 = 420(m)
次郎クンが太郎クンに追いつくのは、次郎クンが家を出てからは 420 / 30 = 14(分)
太郎クンが自宅を出てからは 14 + 6 = 20(分)
x軸 を時間、y軸 を距離としたグラフで次郎クンが追いつく場所 (x,y) を求める
太郎クンが進む 距離/時間の方程式は y = 70x
次郎クンが進む 距離/時間の方程式は y = a * (x - x1) + y1 に速度 a と出発時の (x1,y1) 代入
y = 100(x - 6) + 0 => y = 200x - 600
import sympy as sp
x = sp.Symbol('x')
a = sp.Symbol('a')
x1, y1 = sp.symbols('x1, y1')
y = a * (x - x1) + y1
ty = y.subs({a:70, x1:0, y1:0})
ty
jy = y.subs({a:100, x1:6, y1:0})
jy
直線の交点と連立方程式の解¶
太郎クンの時間/距離の直線式 … y = 70x
次郎クンの時間/距離の直線式 … y = 100x - 60
二つの式を連立方程式として解を求めると
x = sp.Symbol('x')
y = sp.Symbol('y')
ty = sp.Eq(y, 70 * x)
jy = sp.Eq(y, 100 * x - 600)
ans = sp.solve([ty, jy])
ans
{x: 20, y: 1400}
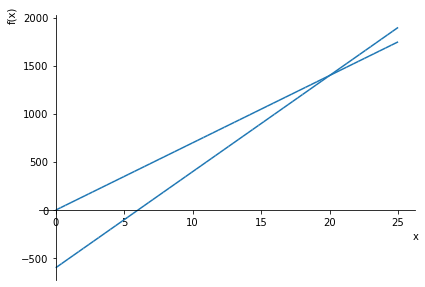
SymPy でグラフを描くと
sp.plot(70 * x, 100 * x - 600, (x, 0, 25))
<sympy.plotting.plot.Plot at 0x181f82bfcd0>